



 (180°-x)=90°-
(180°-x)=90°- x,∠A=180°-x-y.
x,∠A=180°-x-y. x),
x), ∠C.
∠C. ∠C<∠C,这与题设∠C是最小角矛盾.
∠C<∠C,这与题设∠C是最小角矛盾.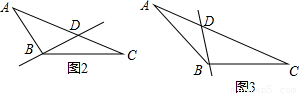
 ∠C.
∠C.

科目:初中数学 来源:2009年江苏省连云港市中考数学原创试卷大赛(40)(解析版) 题型:解答题
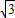 ,1)出发,沿射线OM方向以每秒1个单位长度的速度作匀速运动,在运动过程中,以OP为对角线的矩形OAPB的边长OA:OB=1:
,1)出发,沿射线OM方向以每秒1个单位长度的速度作匀速运动,在运动过程中,以OP为对角线的矩形OAPB的边长OA:OB=1: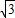 ;过点O且垂直于射线OM的直线l与点P同时出发,且与点P沿相同的方向、以相同的速度运动.
;过点O且垂直于射线OM的直线l与点P同时出发,且与点P沿相同的方向、以相同的速度运动.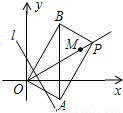
查看答案和解析>>
科目:初中数学 来源:2007年全国中考数学试题汇编《概率》(06)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2007年江苏省无锡市中考数学试卷(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com