
 如图,正三角形ABC的边长是2,分别以点B,C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当r=$\sqrt{2}$时,S为$\frac{π}{2}$-1.
如图,正三角形ABC的边长是2,分别以点B,C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当r=$\sqrt{2}$时,S为$\frac{π}{2}$-1. 分析 首先求出S关于r的函数表达式,分析其增减性;然后根据r的取值,求出S的最大值与最小值,从而得到S的取值.
解答  解:如右图所示,过点D作DG⊥BC于点G,易知G为BC的中点,CG=1,
解:如右图所示,过点D作DG⊥BC于点G,易知G为BC的中点,CG=1,
在Rt△CDG中,由勾股定理得:DG=$\sqrt{C{D}^{2}-C{G}^{2}}$=$\sqrt{{r}^{2}-1}$,
设∠DCG=θ,则由题意可得:
S=2(S扇形CDE-S△CDG)=2($\frac{θ•{r}^{2}}{360}$-$\frac{1}{2}$×1×$\sqrt{{r}^{2}-1}$)=$\frac{θπ{r}^{2}}{180}$-$\sqrt{{r}^{2}-1}$,
∴S=$\frac{θπ{r}^{2}}{180}$-$\sqrt{{r}^{2}-1}$.
当r增大时,∠DCG=θ随之增大,故S随r的增大而增大.
当r=$\sqrt{2}$时,DG=1,∵CG=1,故θ=45°,
∴S=$\frac{45π•(\sqrt{2})^{2}}{180}$-$\sqrt{(\sqrt{2})^{2}-1}$=$\frac{π}{2}$-1,
故答案为:$\frac{π}{2}$-1.
点评 本题考查扇形面积的计算、等边三角形的性质、勾股定理等重要知识点.解题关键是求出S的函数表达式.


科目:初中数学 来源: 题型:解答题
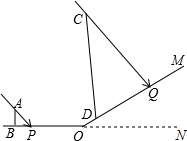 在一个阳光明媚的上午,数学陈老师组织学生测量小山坡的一颗大树CD的高度,山坡OM与地面ON的夹角为30°(∠MON=30°),站立在水平地面上身高1.7米的小明AB在地面的影长BP为1.2米,此刻大树CD在斜坡的影长DQ为5米,求大树的高度.
在一个阳光明媚的上午,数学陈老师组织学生测量小山坡的一颗大树CD的高度,山坡OM与地面ON的夹角为30°(∠MON=30°),站立在水平地面上身高1.7米的小明AB在地面的影长BP为1.2米,此刻大树CD在斜坡的影长DQ为5米,求大树的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
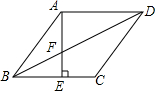 菱形ABCD中,AE⊥BC于E,交BD于F点,下列结论:
菱形ABCD中,AE⊥BC于E,交BD于F点,下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
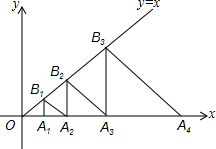 如图,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是等腰直角三角形,其中点A1、A2、…、An在x轴上,点B1、B2、…、Bn在直线y=x上,已知OA2=1,则OA2016的长为22014.
如图,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是等腰直角三角形,其中点A1、A2、…、An在x轴上,点B1、B2、…、Bn在直线y=x上,已知OA2=1,则OA2016的长为22014.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com