如图，自△ABC内的任一点P，作三角形三条边的垂线：PD⊥BC，PE⊥CA，PF⊥AB，若BD=BF，CD=CE．
证明：AE=AF．

证明：
如图，若四边形的两条对角线互相垂直，则其两组对边的平方和相等．
连PA，PB，PC，
则有PA²+BF²=PB²+AF²；
PB²+CD²=PC²+BD²，
PC²+AE²=PA²+CE²；
三式相加得AE²+CD²+BF²=AF²+CE²+BD²，
利用条件BD=BF，CD=CE，
代入上式，得AE=AF．
分析：根据四边形的两条对角线互相垂直，则其两组对边的平方和相等，PA²+BF²=PB²+AF²；PB²+CD²=PC²+BD²，PC²+AE²=PA²+CE²；
代入BD=BF，CD=CE得：AE=AF．
点评：本题考查了勾股定理的正确运用，本题中准确的计算AE²+CD²+BF²=AF²+CE²+BD²是证明AE=AF的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

14、如图，自△ABC内的任一点P，作三角形三条边的垂线：PD⊥BC，PE⊥CA，PF⊥AB，若BD=BF，CD=CE；
证明：AE=AF．

查看答案和解析>>

科目：初中数学 来源： 题型：

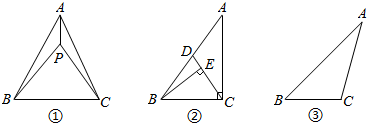
如图①，P为△ABC内一点，连接PA、PB、PC，在△PAB、△PBC和△PAC中，如果存在一个三角形与△ABC相似，那么就称P为△ABC的自相似点．
（1）如图②，已知Rt△ABC中，∠ACB=90°，∠ABC＞∠A，CD是AB上的中线，过点B作BE丄CD，垂足为E．试说明E是△ABC的自相似点；
（2）在△ABC中，∠A＜∠B＜∠C．
①如图③，利用尺规作出△ABC的自相似点P（写出作法并保留作图痕迹）；
②若△ABC的内心P是该三角形的自相似点，求该三角形三个内角的度数．