
【题目】如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
试题分析:根据勾股定理的逆定理可以证明∠BAC=90°;根据直角三角形斜边上的中线等于斜边的一半,则AM=![]() EF,要求AM的最小值,即求EF的最小值;根据三个角都是直角的四边形是矩形,得四边形AEPF是矩形,根据矩形的对角线相等,得EF=AP,则EF的最小值即为AP的最小值,根据垂线段最短,知:AP的最小值即等于直角三角形ABC斜边上的高.
EF,要求AM的最小值,即求EF的最小值;根据三个角都是直角的四边形是矩形,得四边形AEPF是矩形,根据矩形的对角线相等,得EF=AP,则EF的最小值即为AP的最小值,根据垂线段最短,知:AP的最小值即等于直角三角形ABC斜边上的高.
解:∵在△ABC中,AB=3,AC=4,BC=5,
∴AB2+AC2=BC2,
即∠BAC=90°.
又∵PE⊥AB于E,PF⊥AC于F,
∴四边形AEPF是矩形,
∴EF=AP.
∵M是EF的中点,
∴AM=![]() EF=
EF=![]() AP.
AP.
因为AP的最小值即为直角三角形ABC斜边上的高,即等于![]() ,
,
∴AM的最小值是![]() .
.
故选D.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】如图1,A1B1和A2B2是水面上相邻的两条赛道(看成两条互相平行的线段).甲是一名游泳运动健将,乙是一名游泳爱好者,甲在赛道A1B1上从A1处出发,到达B1后,以同样的速度返回A1处,然后重复上述过程;乙在赛道A2B2上以2m/s的速度从B2处出发,到达A2后以相同的速度回到B2处,然后重复上述过程(不考虑每次折返时的减速和转向时间).若甲、乙两人同时出发,设离开池边B1B2的距离为y(m),运动时间为t(s),甲游动时,y(m)与t(s)的函数图象如图2所示.

(1)赛道的长度是 m,甲的速度是 m/s;
(2)分别写出甲在0≤t≤20和20<t≤40时,y关于t的函数关系式:当0≤t≤20,y= ; 当20<t≤40时,y= ;
(3)在图2中画出乙在2分钟内的函数大致图象(用虚线画);
(4)请你根据(3)中所画的图象直接判断,若从甲、乙两人同时开始出发到2分钟为止,甲、乙共相遇了几次?2分钟时,乙距池边B1B2的距离为多少米。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明为了解本班全体同学在阅读方面的情况,采取全面调查的方法,从喜欢阅读“科普常识、小说、漫画、营养美食”等四类图书中调查了全班学生的阅读情况(要求每位学生只能选择一种自己喜欢阅读的图书类型)根据调查的结果绘制了下面两幅不完整的统计图,如图所示:

请你根据图中提供的信息解答下列问题:
(1)该班的学生人数为________人,并把条形统计图补充完整;
(2)在扇形统计图中,表示“漫画”类所对圆心角是________度,喜欢阅读“营养美食”类图书的人数占全班人数的百分比为_______;
(3)如果喜欢阅读“营养美食”类图书的4 名学生中有3名男生和1名女生,现在打算从中随机选出2名学生参加学校组织的“营养美食”知识大赛,请用列表或画树状图的方法,求选出的2名学生中恰好有1名男生和1名女生的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的有( )
①最大的负整数是﹣1;
②数轴上表示﹣3和3的点到原点的距离相等;
③1.32×104是精确到百分位;
④a+6一定比a大;
⑤(﹣2)4与﹣24结果相等.
A. 2个 B. 3个 C. 4个 D. 0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】太仓港区道路绿化工程工地有大量货物需要运输,某车队有载重量为8吨和10吨的卡车共15辆,所有车辆运输一次能运输128吨货物.
(1)求该车队载重量为8吨、10吨的卡车各有多少辆?
(2)随着工程的扩大,车队需要一次运输货物170吨以上,为了完成任务,车队准备增购这两种卡车共5辆(两种车都购买),请写出所有可能的购车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】晚饭后,郑大爷出去散步,如图描述了他散步过程中离家的距离s(米)与散步所用时间t(分)之间的关系,依据图象,下面的描述符合郑大爷散步情景的是( )
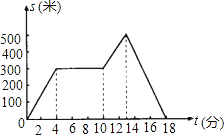
A.从家出发,到了一个公共阅报栏,看了一会儿报,就回家了
B.从家出发,到了一个公共阅报栏,看了一会儿报,继续向前一段,然后回家了
C.从家出发,一直散步(没有停留),然后回家了
D.从家出发,散了一会儿步,就找朋友去了,13分后才开始返回
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com