
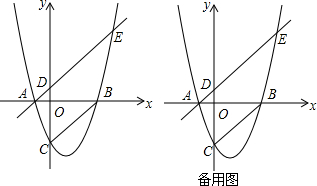
分析 (1)只需把x=0代入抛物线的解析式,就可求出点C的坐标;
(2)①只需先求出直线AE的解析式,再求出直线AE与抛物线的交点坐标,就可解决问题;②由AE∥BC可得∠EAB=∠ABC,然后分△PBC∽△BAE和△PBC∽△EAB两种情况进行讨论,运用相似三角形的性质即可解决问题;
(3)由OQ⊥BQ可知点Q在以OB为直径的圆上,由于直线AE上存在唯一的一点Q,使得OQ⊥BQ,因此以OB为直径的圆与直线AE相切,切点为Q,圆心记为O′,连接O′Q,如图2,易证△AQO′∽△BOC,然后只需用k的代数式表示OC、QO′、AO′、BC,再运用相似三角形的性质就可求出k的值.
解答 解:(1)当x=0时,y=k(0+1)(0-3k)=-3k2,
∴点C的坐标为(0,-3k2).
故答案为:-3k2;
(2)①∵k=1,
∴抛物线的解析式为y=(x+1)(x-3).
当x=0时,y=-3,则点C(0,-3),OC=3;
当y=0时,x1=-1,x2=3,
则点A(-1,0),点B(3,0),OA=1,OB=3.
∵AE∥CB,∴△AOD∽△BOC,
∴$\frac{OD}{OC}$=$\frac{OA}{OB}$,
∴OD=1,即D(0,1).
设直线AE的解析式为y=kx+b,
则$\left\{\begin{array}{l}{-k+b=0}\\{b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$,
∴直线AE的解析式为y=x+1,
联立$\left\{\begin{array}{l}{y=x+1}\\{y=(x+1)(x-3)}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=4}\\{y=5}\end{array}\right.$,
∴点E的坐标为(4,5);
②过点E作EH⊥x轴于H,如图1,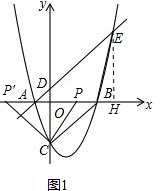
则OH=4,BH=5,AH=5,AE=$\sqrt{{5}^{2}+{5}^{2}}$=5$\sqrt{2}$.
∵AE∥BC,∴∠EAB=∠ABC.
Ⅰ.若△PBC∽△BAE,则$\frac{BP}{AB}$=$\frac{BC}{AE}$.
∵AB=4,BC=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,AE=5$\sqrt{2}$,
∴$\frac{BP}{4}$=$\frac{3\sqrt{2}}{5\sqrt{2}}$,
∴BP=$\frac{12}{5}$,
∴点P的坐标为(3-$\frac{12}{5}$,0)即($\frac{3}{5}$,0);
Ⅱ.若△PBC∽△EAB,则$\frac{BP}{AE}$=$\frac{BC}{AB}$,
∴$\frac{BP}{5\sqrt{2}}$=$\frac{3\sqrt{2}}{4}$,
∴BP=$\frac{15}{2}$,
∴点P的坐标为(3-$\frac{15}{2}$,0)即(-$\frac{9}{2}$,0);
综上所述:满足条件的P点坐标为($\frac{3}{5}$,0)或(-$\frac{9}{2}$,0);
(3)∵直线AE上存在唯一的一点Q,使得OQ⊥BQ,
∴以OB为直径的圆与直线AE相切于点Q,圆心记为O′,连接O′Q,如图2,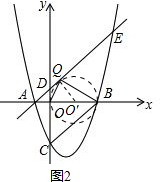
则有O′Q⊥AE,O′Q=OO′=$\frac{1}{2}$OB.
当x=0时,y=k(0+1)(0-3k)=-3k2,则点C(0,-3k2),
当y=0时,k(x+1)(x-3k)=0,解得x1=-1,x2=3k,
则点A(-1,0),B(3k,0),
∴OB=3k,OA=1,OC=3k2,
∴O′Q=OO′=$\frac{3k}{2}$,O′A=$\frac{3k}{2}$+1,BC=$\sqrt{(3{k}^{2})^{2}+(3k)^{2}}$=3k•$\sqrt{{k}^{2}+1}$.
∵∠QAO′=∠OBC,∠AQO′=∠BOC=90°,
∴△AQO′∽△BOC,
∴$\frac{QO′}{OC}$=$\frac{AO′}{BC}$,
∴QO′•BC=AO′•OC,
∴$\frac{3k}{2}$•3k•$\sqrt{{k}^{2}+1}$=($\frac{3k}{2}$+1)•3k2,
解得:k=$\frac{5}{12}$.
点评 本题主要考查了相似三角形的判定与性质、圆周角定理、抛物线上点的坐标特征、运用待定系数法求直线的解析式、求直线与抛物线的交点坐标、勾股定理等知识,解决第3小题的关键是把条件转化为以OB为直径的圆与直线AE相切.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{(-2)^{2}}$=-2 | B. | (-$\sqrt{3}$)2=9 | C. | $\root{3}{-9}$=-3 | D. | ±$\sqrt{9}$=±3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
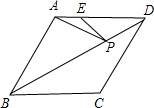 如图,在菱形ABCD中,AB=6,∠ABC=60°,点E在AD上,且AE=2,点P是对角线BD上的一个动点,则PE+PA的最小值是2$\sqrt{7}$.
如图,在菱形ABCD中,AB=6,∠ABC=60°,点E在AD上,且AE=2,点P是对角线BD上的一个动点,则PE+PA的最小值是2$\sqrt{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4.79×107 | B. | 4.79×108 | C. | 4.79×109 | D. | 4.79×1010 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com