
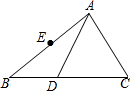
 如图,△ABC中,D为BC边上的点,∠CAD=∠CDA,E为AB边的中点.
如图,△ABC中,D为BC边上的点,∠CAD=∠CDA,E为AB边的中点.分析 (1)根据角平分线的作图可得;
(2)由等腰三角形的三线合一,结合E为AB边的中点证EF为△ABD的中位线可得;
(3)利用相似三角形的性质可得.
解答 解:(1)如图,射线CF即为所求;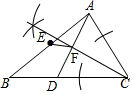
(2)EF∥BC.
∵∠CAD=∠CDA,
∴AC=DC,即△CAD为等腰三角形;
又CF是顶角∠ACD的平分线,
∴CF是底边AD的中线,即F为AD的中点,
∵E是AB的中点,
∴EF为△ABD的中位线,
∴EF∥BD,从而EF∥BC;
(3)由(2)知EF∥BC,
∴△AEF∽△ABD,
∴$\frac{{{S_{△AEF}}}}{{{S_{△ABD}}}}={(\frac{AE}{AB})^2}$,
又∵AE=$\frac{1}{2}$AB,
∴得$\frac{{S}_{△AEF}}{{S}_{△AEF}+{S}_{四边形BDFE}}$=$\frac{1}{4}$,
把S四边形BDFE=9代入其中,解得S△AEF=3,
∴S△ABD=S△AEF+S四边形BDFE=3+9=12,
即△ABD的面积为12.
点评 本题主要考查作图-基本作图和等腰三角形的性质、中位线定理及相似三角形的判定与性质,熟练掌握等腰三角形的性质、中位线定理及相似三角形的判定与性质是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3x}$与$\frac{a}{6{x}^{2}}$最简公分母是6x2 | |
| B. | $\frac{1}{m+n}$与$\frac{1}{m-n}$的最简公分母是(m+n)(m-n) | |
| C. | $\frac{1}{3{a}^{2}{b}^{3}}$与$\frac{1}{3{a}^{2}{b}^{3}c}$最简公分母是3a2b3c | |
| D. | $\frac{1}{a(x-y)}$与$\frac{1}{b(y-x)}$的最简公分母是ab(x-y)(y-x) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 探索与发现
探索与发现查看答案和解析>>
科目:初中数学 来源: 题型:填空题
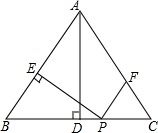 如图,在等腰△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,动点P从点B出发沿BC方向以每秒5个单位的速度向终点C运动,过点P作PE⊥AB于点E,过点P作PF∥BA,交AC于点F,设点P运动的时间为t秒.若以PE所在的直线为对称轴,线段BD经轴对称变换后的图形为B'D',求当线段B'D'与线段AC有交点这段过程中,线段B'D'扫过的面积$\frac{66}{25}$.
如图,在等腰△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,动点P从点B出发沿BC方向以每秒5个单位的速度向终点C运动,过点P作PE⊥AB于点E,过点P作PF∥BA,交AC于点F,设点P运动的时间为t秒.若以PE所在的直线为对称轴,线段BD经轴对称变换后的图形为B'D',求当线段B'D'与线段AC有交点这段过程中,线段B'D'扫过的面积$\frac{66}{25}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
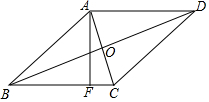 如图,在菱形ABCD中,对角线AC、BD交于点O,AF⊥BC于点F,若AC=2,BD=6,则AF=$\frac{3\sqrt{10}}{5}$.
如图,在菱形ABCD中,对角线AC、BD交于点O,AF⊥BC于点F,若AC=2,BD=6,则AF=$\frac{3\sqrt{10}}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com