
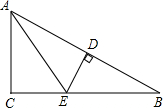
 如图,∠ACB=90°,DE垂直平分AB,∠CAE=∠EAB,求∠B的度数.
如图,∠ACB=90°,DE垂直平分AB,∠CAE=∠EAB,求∠B的度数.  小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:解答题
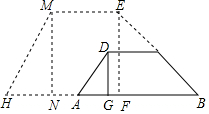 如图,拦水坝的横断面为梯形ABCD,AB∥CD,坝顶宽DC为6米,坝高DG为2米,迎水坡BC的坡角为30°,坝底宽AB为(8+2$\sqrt{3}$)米.
如图,拦水坝的横断面为梯形ABCD,AB∥CD,坝顶宽DC为6米,坝高DG为2米,迎水坡BC的坡角为30°,坝底宽AB为(8+2$\sqrt{3}$)米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
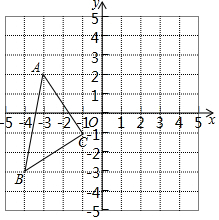 如图,在平面直角坐标系XOY中,A(-3,2),B(-4,-3),C(-1,-1)
如图,在平面直角坐标系XOY中,A(-3,2),B(-4,-3),C(-1,-1)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=$\frac{1}{2}$x+2与x轴和y轴分别相交于A、B两点,把△AOB绕原点顺时针旋转90°得到△COD,且抛物线y=ax2b+x+c过A、C、D三点.
如图,直线y=$\frac{1}{2}$x+2与x轴和y轴分别相交于A、B两点,把△AOB绕原点顺时针旋转90°得到△COD,且抛物线y=ax2b+x+c过A、C、D三点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
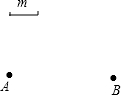 如图,已知平面内A,B两点和线段m.
如图,已知平面内A,B两点和线段m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
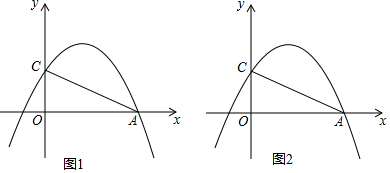
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com