
已知:直线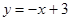 交
交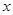 轴于点
轴于点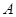 ,交
,交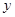 轴于点
轴于点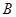 ,抛物线
,抛物线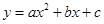 经过
经过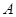 、
、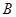 、
、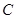 (1,0)三点.
(1,0)三点.
(1)求抛物线的解析式;
(2)若点 的坐标为(-1,0),在直线
的坐标为(-1,0),在直线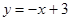 上有一点
上有一点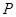 ,使
,使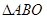 与
与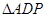 相似,求出点
相似,求出点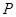 的坐标;
的坐标;
(3)在(2)的条件下,在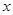 轴下方的抛物线上,是否存在点
轴下方的抛物线上,是否存在点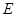 ,使
,使 的面积等于四边形
的面积等于四边形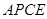 的面积?如果存在,请求出点
的面积?如果存在,请求出点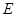 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
(1) ;(2)
;(2)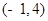 或(1,2);(3)不存在
或(1,2);(3)不存在
【解析】
试题分析:(1)先求得直线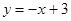 与坐标轴的交点A、B的坐标,再由抛物线经过A、B、C三点即可根据待定系数法求得结果;
与坐标轴的交点A、B的坐标,再由抛物线经过A、B、C三点即可根据待定系数法求得结果;
(2)由题意可得:△ABO为等腰直角三角形,分△ABO∽△AP1D,△ABO∽△ADP2,根据等腰三角形的性质及相似三角形的性质求解即可;
(3)如图设点E 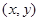 ,根据三角形的面积公式可得
,根据三角形的面积公式可得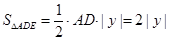 ①当P1(-1,4)时,
①当P1(-1,4)时,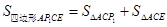
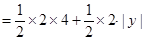 =
= 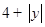 ,由点E在x轴下方可得
,由点E在x轴下方可得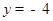 ,代入得
,代入得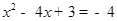 即
即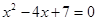 ,根据△=(-4)2-4×7=-12<0可得此方程无解;②当P2(1,2)时,
,根据△=(-4)2-4×7=-12<0可得此方程无解;②当P2(1,2)时,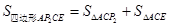 =
= 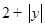 ,由点E在x轴下方可得
,由点E在x轴下方可得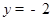 ,代入得:
,代入得: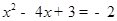 ,即
,即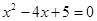 ,根据△=(-4)2-4×5=-4<0可得此方程无解,综上所述,在x轴下方的抛物线上不存在这样的点E.
,根据△=(-4)2-4×5=-4<0可得此方程无解,综上所述,在x轴下方的抛物线上不存在这样的点E.
(1)由题意得,A(3,0),B(0,3)
∵抛物线经过A、B、C三点,
∴把A(3,0),B(0,3),C(1,0)三点分别代入 得方程组
得方程组
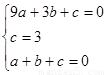 ,解得:
,解得: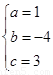
∴抛物线的解析式为 ;
;
(2)由题意可得:△ABO为等腰直角三角形,如图所示
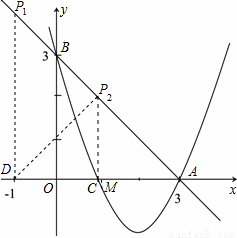
若△ABO∽△AP1D,则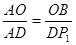
∴DP1=AD=4
∴P1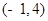
若△ABO∽△ADP2 ,过点P2作P2 M⊥x轴于M,AD=4
∵△ABO为等腰三角形
∴△ADP2是等腰三角形,由三线合一可得:DM="AM=2=" P2M,即点M与点C重合
∴P2(1,2);
(3)如图设点E 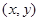 ,则
,则
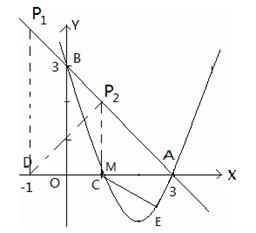
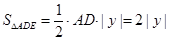
①当P1(-1,4)时,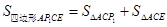
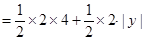 =
= 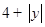
∴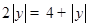 ,
,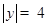
∵点E在x轴下方
∴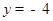 ,代入得
,代入得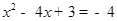 即
即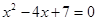
∵△=(-4)2-4×7=-12<0
∴此方程无解;
②当P2(1,2)时,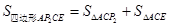 =
= 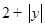
∴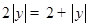 ,
,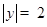
∵点E在x轴下方
∴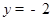 ,代入得:
,代入得: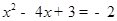 ,即
,即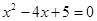 ,
,
∵△=(-4)2-4×5=-4<0
∴此方程无解
综上所述,在x轴下方的抛物线上不存在这样的点E.
考点:二次函数的综合题
点评:此类问题是初中数学的重点和难点,在中考中极为常见,一般以压轴题形式出现,难度较大.


科目:初中数学 来源: 题型:
如图,已知平面直角坐标系![]() 中,点A(2,m),B(-3,n)为两动点,其中m﹥1,连结
中,点A(2,m),B(-3,n)为两动点,其中m﹥1,连结![]() ,
,![]() ,作
,作![]() 轴于
轴于![]() 点,
点,![]() 轴于
轴于![]() 点.
点.
1.求证:mn=6
2.当![]() 时,抛物线经过
时,抛物线经过![]() 两点且以
两点且以![]() 轴为对称轴,求抛物线对应的二次函数的关系式
轴为对称轴,求抛物线对应的二次函数的关系式
3.在(2)的条件下,设直线![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作直线
作直线![]() 交抛物线于
交抛物线于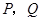 两点,问是否存在直线
两点,问是否存在直线![]() ,使S⊿POF:S⊿QOF=1:2?若存在,求出直线
,使S⊿POF:S⊿QOF=1:2?若存在,求出直线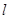 对应的函数关系式;若不存在,请说明理由.
对应的函数关系式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2011-2012年江苏省苏州市九年级第一学期期末考试数学卷 题型:解答题
.(10分)如图,已知抛物线与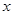 轴交于点
轴交于点 ,
, ,与
,与 轴交于点
轴交于点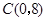 .
.
【小题1】(1)求抛物线的解析式及其顶点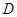 的坐标;
的坐标;
【小题2】(2)设直线 交
交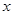 轴于点
轴于点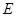 .在线段
.在线段 的垂直平分线上是否存在点
的垂直平分线上是否存在点 ,使得点
,使得点 到直线
到直线 的距离等于点
的距离等于点 到原点
到原点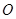 的距离?如果存在,求出点
的距离?如果存在,求出点 的坐标;如果不存在,请说明理由;
的坐标;如果不存在,请说明理由;
【小题3】(3)过点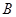 作
作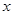 轴的垂线,交直线
轴的垂线,交直线 于点
于点 ,将抛物线沿其对称轴平移,使抛物线与线段
,将抛物线沿其对称轴平移,使抛物线与线段 总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
查看答案和解析>>
科目:初中数学 来源:2013届广西贵港市平南县九年级5月第二次模拟考试数学试卷(带解析) 题型:解答题
已知:直线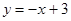 交
交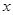 轴于点
轴于点 ,交
,交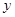 轴于点
轴于点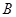 ,抛物线
,抛物线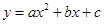 经过
经过 、
、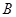 、
、 (1,0)三点.
(1,0)三点.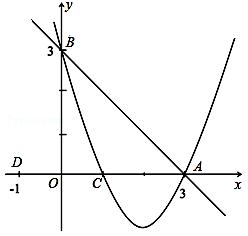
(1)求抛物线的解析式;
(2)若点 的坐标为(-1,0),在直线
的坐标为(-1,0),在直线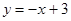 上有一点
上有一点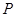 ,使
,使 与
与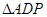 相似,求出点
相似,求出点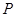 的坐标;
的坐标;
(3)在(2)的条件下,在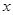 轴下方的抛物线上,是否存在点
轴下方的抛物线上,是否存在点 ,使
,使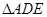 的面积等于四边形
的面积等于四边形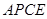 的面积?如果存在,请求出点
的面积?如果存在,请求出点 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2007年初中毕业升学考试(山东潍坊卷)数学(解析版) 题型:解答题
如图,已知平面直角坐标系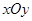 中,点
中,点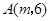 ,
,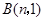 为两动点,其中
为两动点,其中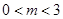 ,连结
,连结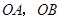 ,
,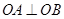 .
.
(1)求证: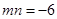 ;
;
(2)当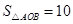 时,抛物线经过
时,抛物线经过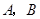 两点且以
两点且以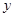 轴为对称轴,求抛物线对应的二次函数的关系式;
轴为对称轴,求抛物线对应的二次函数的关系式;
(3)在(2)的条件下,设直线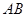 交
交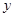 轴于点
轴于点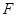 ,过点
,过点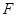 作直线
作直线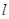 交抛物线于
交抛物线于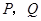 两点,问是否存在直线
两点,问是否存在直线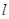 ,使
,使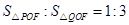 ?若存在,求出直线
?若存在,求出直线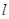 对应的函数关系式;若不存在,请说明理由.
对应的函数关系式;若不存在,请说明理由.
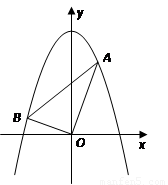
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com