
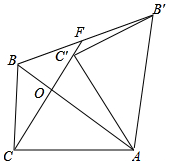
 如图,在Rt△ABC中,∠ACB=90°,tan∠CBA=$\frac{4}{3}$,AB=5.将△ABC绕点A顺时针旋转得到△AB′C′,连接CC′并延长,交AB于点O,交BB′于点F.若CC′=CA,则BF=$\frac{5}{2}$.
如图,在Rt△ABC中,∠ACB=90°,tan∠CBA=$\frac{4}{3}$,AB=5.将△ABC绕点A顺时针旋转得到△AB′C′,连接CC′并延长,交AB于点O,交BB′于点F.若CC′=CA,则BF=$\frac{5}{2}$. 分析 先过O作OH⊥BC于H,根据△BOH∽△BAC,可得$\frac{BO}{OH}$=$\frac{BA}{AC}$=$\frac{5}{4}$,再根据∠HCO=30°,可得OH=$\frac{1}{2}$CO,进而得到$\frac{BO}{CO}$=$\frac{5}{8}$,再判定△BOF∽△COA,可得$\frac{BF}{CA}$=$\frac{BO}{CO}$,即$\frac{BF}{4}$=$\frac{5}{8}$,据此可得BF的长.
解答 解:如图,过O作OH⊥BC于H,
由∠ACB=90°,tan∠CBA=$\frac{4}{3}$,AB=5,可得AC=4,
∵∠ACB=90°=∠OHB,
∴OH∥AC,
∴△BOH∽△BAC,
∴$\frac{BO}{OH}$=$\frac{BA}{AC}$=$\frac{5}{4}$,
由旋转可得CA=C'A,而CC′=CA,
∴△ACC'是等边三角形,
∴∠ACC'=60°,∠CAC'=60°,
∴∠HCO=30°,
∴OH=$\frac{1}{2}$CO,
∴$\frac{BO}{CO}$=$\frac{5}{8}$,
由旋转可得,∠BAB'=∠CAC'=60°,AB=AB',
∴△ABB'是等边三角形,
∴∠ABB'=60°=∠ACO,
又∵∠BOF=∠COA,
∴△BOF∽△COA,
∴$\frac{BF}{CA}$=$\frac{BO}{CO}$,即$\frac{BF}{4}$=$\frac{5}{8}$,
∴BF=$\frac{5}{2}$,
故答案为:$\frac{5}{2}$.
点评 本题主要考查了旋转的性质,相似三角形的判定与性质以及等边三角形的判定与性质的运用,解决问题的关键是作辅助线构造直角三角形,依据相似三角形的对应边成比例进行计算求解.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 等腰三角形 | D. | 直角三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
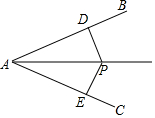 如图,点P在∠BAC的角平分线上,PD⊥AB,PE⊥AC,垂足分别为D、E,则△APD与△APE全等的理由是( )
如图,点P在∠BAC的角平分线上,PD⊥AB,PE⊥AC,垂足分别为D、E,则△APD与△APE全等的理由是( )| A. | SAS | B. | AAS | C. | SSS | D. | HL |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ($\sqrt{6}$)2=±6 | B. | ($\sqrt{-7}$)2=-7 | C. | $\sqrt{3}$×$\sqrt{6}$=3$\sqrt{2}$ | D. | $\sqrt{6}$÷$\sqrt{3}$=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 审核书稿中的错别字 | B. | 调查《极限挑战》栏目的收视率 | ||
| C. | 对八名同学的身高情况进行调查 | D. | 对某社区的卫生死角进行调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com