练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    在平面直角坐标系xOy中，点P（2，a）在正比例函数的图象上，则点Q（a，3a－5）位于第　 　象限．
    四
    待定系数法是求函数关系式的常用方法。把P（2，a）在正比例函数得a=1所以点Q（a，3a－5）坐标为（1，3-5），即为（1，-2），所以在第四象限。
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：不详 题型：单选题

    如图，把Rt△ABC放在直角坐标系内，其中∠CAB=90°， BC=5，点A、B的坐标分别为(1，O)、(4，0)，将△ABC沿x轴向右平移，当点C落在直线y=x-3上时，线段BC扫过的面积为   【 】 

    A. 24          B. 12          C. 6          D.

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    如图，一次函数y="-12" x+4的图象交x轴于点A，交正比例函数y=x的图象于点B．矩形CDEF的边DC在x轴上，D在C的左侧，EF在x轴上方，DC=2，DE=4．当点C坐标为（-2，0）时，矩形CDEF开始以每秒2个单位的速度沿x轴向右运动，运动时间为t秒．

    （1）求点B的坐标．
    （2）矩形CDEF运动t秒时，直接写出C、D两点的坐标．
    （3）当点B在矩形CDEF的一边上时，求t的值．
    （4）设CF、DE分别交折线OBA于M、N两点，当四边形MCDN为直角梯形时，求t的取范围．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    （本题8分）某服装店老板到厂家选购A、B两种型号的服装，它们的进价及获利如右表所示．
    （1）根据市场需求，服装店老板决定，购进B型服装的数量要比购进A型服装数量的2倍少3件，且A型服装最多可购进28件，这样服装全部售出后，可使总的获利不少于1534元．问有几种进货方案？请求出所有的进货方案.
    （2）采用哪种方案时，可获得最大利润，最大利润为多少？
    型号
    		A
    		B
    进价（元/件）
    		90
    		120
    获利（元/件）
    		20
    		22
     

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

     如图，直线l是一次函数y=kx＋b的图象，则有（     ）
     
    A、 k＜0  b＜0   B、 k＜0  b＞0    C、 k＞0  b＞0    D、 k＞0  b＜0

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

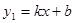    如图，一次函数的图象与反比例函数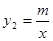的图象交于点A﹙－2，－5﹚，C﹙5，n﹚，交y轴于点B，交x轴于点D．
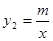    小题1:求反比例函数和一次函数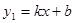的表达式；
    小题2:连接OA，OC．求△AOC的面积．     
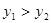    小题3:根据图像，直接写出时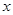的取值范围。

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

    一辆汽车在行驶过程中，路程y (千米)与时间x (小时)之间的函数关系如图6所示．当0≤x≤1时，y关于x的函数关系式为y=60x，那么当1≤x≤2时，y关于x的函数关系式为　                      ．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    一次函数y=kx+b的图象如图所示，当x>4时，y的取值范围是
    A．y<-3B．y<3C．y>3D．y>-3

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

    如图，点A的坐标为(－1,0)，点B在直线y=x上运动，当线段AB最短时，点B的坐标为_________。

    查看答案和解析>>

    同步练习册答案