
已知:如图,在梯形ABCD中,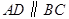 ,AB=DC。点E,F,G分别在边AB,BC,CD上,AE=GF=GC。
,AB=DC。点E,F,G分别在边AB,BC,CD上,AE=GF=GC。

(1)求证:四边形AEFG是平行四边形;
(2)当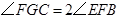 时,求证:四边形AEFG是矩形。
时,求证:四边形AEFG是矩形。
(1)可证明GF∥AE∵GF=AE
∴四边形AEFG是平行四边形(2)可证明∠EFG=90°∴□AEFG是矩形
【解析】
试题分析:证明:(1)∵FG=CG
∴∠1=∠C
∵四边形ABCD是等腰梯形
∴∠B=∠C
∴∠1=∠C
∴GF∥AE
∵GF=AE
∴四边形AEFG是平行四边形
(2)作GH⊥FC
∵GF=GC
∴∠FGC=2∠GFH
∵∠GFC=2∠EFB
∴∠GFH=∠EFB
∵∠GFH+∠FGH=90°
∴∠EFB+∠GFH=90°
∴∠EFG=90°
∴□AEFG是矩形
考点:特殊四边形
点评:本题难度中等,主要考查学生对特殊四边形的性质定理的掌握。根据判定定理进行求证即可。


科目:初中数学 来源: 题型:
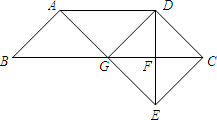 (2013•闵行区二模)已知:如图,在梯形ABCD中,AD∥BC,AB=CD,BC=2AD.DE⊥BC,垂足为点F,且F是DE的中点,联结AE,交边BC于点G.
(2013•闵行区二模)已知:如图,在梯形ABCD中,AD∥BC,AB=CD,BC=2AD.DE⊥BC,垂足为点F,且F是DE的中点,联结AE,交边BC于点G.| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,在梯形ABCD中,AD∥BC,CD=10cm,∠B=45度,∠C=30度,AD=5cm.
已知:如图,在梯形ABCD中,AD∥BC,CD=10cm,∠B=45度,∠C=30度,AD=5cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com