
 如图,在直角坐标系中,△AOB是边长为2的等边三角形,设直线x=t(0≤t≤2)截这个三角形可得位于此直线左方的图形的面积为y,则y关于t的函数图象大致是
如图,在直角坐标系中,△AOB是边长为2的等边三角形,设直线x=t(0≤t≤2)截这个三角形可得位于此直线左方的图形的面积为y,则y关于t的函数图象大致是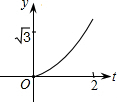
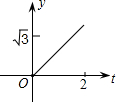
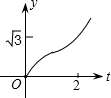
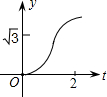
 t;最后根据三角形的面积公式,解答出y与t之间的函数关系式,由函数解析式来选择图象.
t;最后根据三角形的面积公式,解答出y与t之间的函数关系式,由函数解析式来选择图象.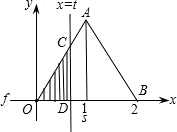
 t;
t; ×OD×CD
×OD×CD t2(0≤t≤1),
t2(0≤t≤1), t2(0≤t≤1).
t2(0≤t≤1).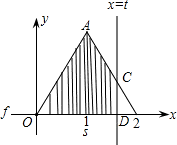
 (2-t);
(2-t); ×BD×CD
×BD×CD (2-t)2(0≤t≤1),
(2-t)2(0≤t≤1), -
- (2-t)2(0≤t≤1)=.
(2-t)2(0≤t≤1)=.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′. | PP′ |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 6 |
| x |
| 3 |
| 2 |
| 6 |
| x |

查看答案和解析>>
科目:初中数学 来源: 题型:
 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com