
| 业务种类 | 计费单位 | 资费标准/元 | |
| 本埠资费 | 外埠资费 | ||
| 信函 | 首重100克内,每重20克(不足20克按20克计算) | 0.80 | 1.20 |
| 续重101-2000克每重100克(不足100克按100克计算) | 1.20 | 2.00 | |
分析 我们把信函重量进行划类,看看在那一行列,再列式进行计算即可.
(1)75克看作4个20克进行计算即可.
(2)145克看作5个20克+45克,进行解答即可;
(3)250克看作5个20克+100克+50克,算出邮费,解析解答即可.
解答 解:(1)75÷20=3…15(克),
3+1=4
4×0.8=3.2(元)
1.2+1.2+0.8=3.2(元),
∴选2张1.2元和1张0.8元的邮票.
(2)145=5×20+45,
5×0.8+1.2=4+1.2=5.2(元),
2×2+1.2=5.2(元),
2+1.2×2+0.8=5.2(元)
∴选2张2元和1张1.2元的邮票或选1张2元、2张1.2元和1张0.8元.
(3)250=100+150,
5×1.2+2×2=10(元)
4×2+1.2+0.8=10(元)
∴选2张4元、1张1.2元、1张0.8元的邮票.
点评 本题与实际生活紧密相连,主要考查实际问题实际分析,分类讨论、解决问题的能力本题关键读懂统计表,再根据题意进行解答即可.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1)(4) | B. | (1)(2) | C. | (2)(3) | D. | (3)(4) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
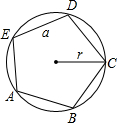 圆的内接正五边形ABCDE的边长为a,圆的半径为r.下列等式成立的是( )
圆的内接正五边形ABCDE的边长为a,圆的半径为r.下列等式成立的是( )| A. | a=2rsin36° | B. | a=2rcos36° | C. | a=rsin36° | D. | a=2rsin72° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
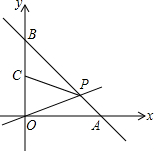 已知一次函数y=kx-2k+3(k<0)的图象与x轴交于点A,与y轴交于点B.
已知一次函数y=kx-2k+3(k<0)的图象与x轴交于点A,与y轴交于点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
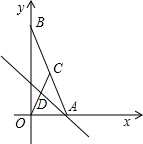 如图,在平面直角坐标系中,直线y=-2x+12与x轴、y轴交于A、B两点,点C是线段AB的中点,点D在线段OC上,OD=2CD.
如图,在平面直角坐标系中,直线y=-2x+12与x轴、y轴交于A、B两点,点C是线段AB的中点,点D在线段OC上,OD=2CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
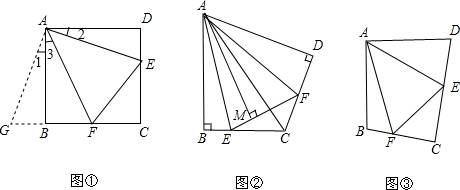
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com