
 如图,在菱形ABCD中,E是AB的中点,且DE⊥AB,
如图,在菱形ABCD中,E是AB的中点,且DE⊥AB,科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
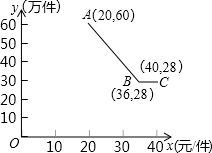 淮安华宇公司获得授权生产某种奥运纪念品,经市场调查分析,该纪念品的销售量y1(万件)与纪念品的价格x(元/件)之间的函数图象如图,该公司纪念品的生产数量y2(万件)与纪念品的价格x(元/件)近似满足函数关系式y2=-
淮安华宇公司获得授权生产某种奥运纪念品,经市场调查分析,该纪念品的销售量y1(万件)与纪念品的价格x(元/件)之间的函数图象如图,该公司纪念品的生产数量y2(万件)与纪念品的价格x(元/件)近似满足函数关系式y2=-| 3 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com