
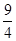 ;(2)S=
;(2)S=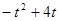 ,当
,当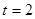 时,S最大值=4;(3)
时,S最大值=4;(3)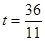 和
和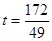
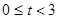 和
和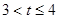 两种情况,结合相似三角形的判定方法讨论即可.
两种情况,结合相似三角形的判定方法讨论即可.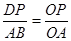
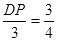
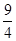 ;
;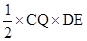 =
=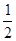 ×2t×(4–t)=
×2t×(4–t)=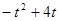
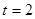 时,S最大值=4
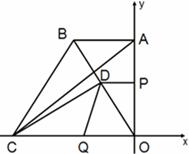
时,S最大值=4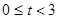 时,点Q在CO上运动(当t=3时,△ODQ不存在)
时,点Q在CO上运动(当t=3时,△ODQ不存在)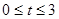 时,△ODQ与△ABC不可能相似。
时,△ODQ与△ABC不可能相似。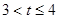 时,点Q在x轴正半轴上运动,
时,点Q在x轴正半轴上运动,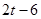 ,由DP∥AB可得OD=
,由DP∥AB可得OD=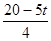
 时,
时,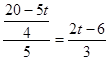 ,
,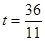 在
在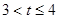 内;
内;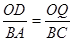 时,
时,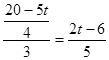 ,
,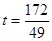 在
在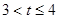 内;
内;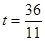 和
和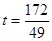 ,使△ODQ与△ABC相似。
,使△ODQ与△ABC相似。

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:解答题
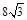 米.请你建立适当的平面直角坐标系解决下列问题.
米.请你建立适当的平面直角坐标系解决下列问题. 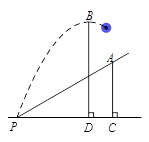
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 价格y1(元/件) | 560 | 580 | 600 | 620 | 640 | 660 | 680 | 700 | 720 |
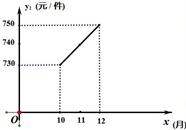
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.二次函数图像的对称轴是直线x=1; |
| B.当x>0时,y<4; |
| C.当x≤1时,函数值y是随着x的增大而增大; |
| D.当y≥0时,x的取值范围是-1≤x≤3时. |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
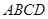 中,
中,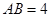 cm,
cm,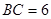 cm,现有一动点
cm,现有一动点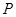 从
从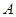 出发以2cm/秒的速度,沿矩形的边
出发以2cm/秒的速度,沿矩形的边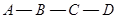 回到点
回到点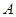 ,设点
,设点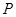 运动的时间为
运动的时间为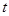 秒.
秒.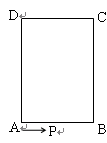
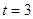 秒时,求
秒时,求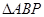 的面积;
的面积;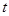 为何值时,点
为何值时,点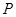 与点
与点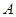 的距离为5cm?
的距离为5cm?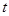 为何值时
为何值时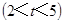 ,以线段
,以线段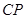 、
、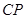 、
、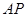 的长度为三边长的三角形是直角三角形,且
的长度为三边长的三角形是直角三角形,且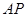 是斜边.
是斜边.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com