
科目:初中数学 来源: 题型:
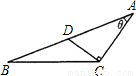
 13、如图,在一场足球比赛中,球员A欲传球给同伴B,对方球员C意图抢断传球,已知球速为16m/s,球员速度为8m/s.当球由A传出的同时,球员C选择与AC垂直的方向出击,恰好在点D处将球成功抢断,则角θ=
13、如图,在一场足球比赛中,球员A欲传球给同伴B,对方球员C意图抢断传球,已知球速为16m/s,球员速度为8m/s.当球由A传出的同时,球员C选择与AC垂直的方向出击,恰好在点D处将球成功抢断,则角θ=查看答案和解析>>
科目:初中数学 来源: 题型:
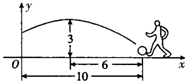 (2013•鞍山二模)在一场足球比赛中,一球员从球门正前方10米处起脚射门,当球飞行的水平距离为6米时达到最高点,此时球高为3米.
(2013•鞍山二模)在一场足球比赛中,一球员从球门正前方10米处起脚射门,当球飞行的水平距离为6米时达到最高点,此时球高为3米.查看答案和解析>>
科目:初中数学 来源: 题型:044
在某场足球比赛中,一球员将球从球门正前方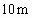 的点O处将球踢起,沿垂直于球门的方向飞向球门.球的飞行路线是抛物线的一部分,如图所示.抛物线的解析式为
的点O处将球踢起,沿垂直于球门的方向飞向球门.球的飞行路线是抛物线的一部分,如图所示.抛物线的解析式为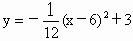 ,已知球门高2.44m,该球能否被射入球门?
,已知球门高2.44m,该球能否被射入球门?

查看答案和解析>>
科目:初中数学 来源:2004年湖北省荆州市中考数学试卷(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com