
分析 (1)设商场购进甲型节能灯x只,则购进乙型节能灯(1200-x)只,根据两种节能灯的总价为46000元建立方程求出其解即可;
(2)设商场购进甲型节能灯a只,则购进乙型节能灯(1200-a)只,商场的获利为y元,由销售问题的数量关系建立y与a的解析式就可以求出结论.
解答 解:(1)设商场购进甲型节能灯x只,则购进乙型节能灯(1200-x)只,由题意,得
25x+45(1200-x)=46000,
解得:x=400.
∴购进乙型节能灯1200-400=800(只).
答:购进甲型节能灯400只,购进乙型节能灯800只进货款恰好为46000元;
(2)设商场购进甲型节能灯a只,则购进乙型节能灯(1200-a)只,商场的获利为y元,由题意,得
y=(30-25)a+(60-45)(1200-a),
y=-10a+18000.
∵商场销售完节能灯时获利最多且不超过进货价的30%,
∴-10a+18000≤[25a+45(1200-a)]×30%,
∴a≥450.
∵y=-10a+18000,
∴k=-10<0,
∴y随a的增大而减小,
∴a=450时,y最大=13500元.
∴商场购进甲型节能灯450只,购进乙型节能灯750只时的最大利润为13500元.
点评 本题考查了单价×数量=总价的运用,列了一元一次方程解实际问题的运用,一次函数的解析式的运用,解答时求出一次函数的解析式是关键.


科目:初中数学 来源: 题型:选择题
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
| A. | 抛物线于x轴的一个交点坐标为(-2,0) | |
| B. | 抛物线与y轴的交点坐标为(0,6) | |
| C. | 抛物线的对称轴是直线x=0 | |
| D. | 抛物线在对称轴左侧部分是上升的 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 方案 | 间隔长(米) | 应植树数(棵) | 路长(米) |
| 方案1 | 5 | ( ) | ( ) |
| 方案2 | 5.5 | ( x ) | ( ) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
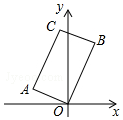 如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,则B点的坐标分别是( )
如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,则B点的坐标分别是( )| A. | ($\frac{3}{2}$,3) | B. | ($\frac{3}{2}$,4) | C. | ($\frac{7}{4}$,4) | D. | ($\frac{7}{4}$,$\frac{7}{2}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com