
【题目】化简下列多项式:
(1)![]()
(2)![]()
(3)若![]() ,求
,求![]() 的值.
的值.
(4)先化简,再求值:(2x﹣1)2﹣(3x+1)(3x﹣1)+5x(x﹣1),其中x=﹣2.
科目:初中数学 来源: 题型:
【题目】如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠1=∠2,
(1)试判断DG与BC的位置关系,并说明理由.
(2)若∠A=70°,∠BCG=40°,求∠AGD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
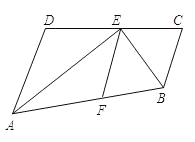
【题目】如图,点E在线段CD上,EA、EB分别平分∠DAB和∠CBA,点F在线段AB上运动,AD=4cm,BC=3cm,且AD∥BC.
(1)你认为AE和BE有什么位置关系?并验证你的结论;
(2)当点F运动到离点A多少厘米时,△ADE和△AFE全等?为什么?
(3)在(2)的情况下,此时BF=BC吗?证明你的结论并求出AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD∥CB,∠A=∠C,若∠ABD=32°,求∠BDC的度数.有同学用了下面的方法.但由于一时犯急没有写完整,请你帮他添写完整.
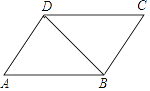
解:∵AD∥CB(已知)
∴∠C+∠ADC=180°(_________________),
又∵∠A=∠C (___________________),
∴∠A+∠ADC=180° (___________________),
∴AB∥CD (___________________________),
∴∠BDC=∠ABD=32° (___________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接2008年北京奥运会,某学校组织了一次野外长跑活动,参加长跑的同学出发后,另一些同学从同地骑自行车前去加油助威。如图,线段L1,L2分别表示长跑的同学和骑自行车的同学行进的路程y(千米)随时间x(分钟)变化的函数图象.根据图象,解答下列问题:
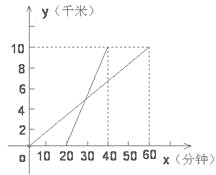
(1)分别求出长跑的同学和骑自行车的同学的行进路程y与时间x的函数表达式;
(2)求长跑的同学出发多少时间后,骑自行车的同学就追上了长跑的同学?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )
实验次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 2000 |
频率 | 0.365 | 0.328 | 0.330 | 0.334 | 0.336 | 0.332 | 0.333 |
A.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
B.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
C.抛一个质地均匀的正六面体骰子,向上的面点数是5
D.抛一枚硬币,出现反面的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,已知点C在线段AB上,且AC=6cm,BC=4cm,点M,N分别是AC,BC的中点,求线段MN的长度.
![]()
(2)在(1)中,如果AC=acm,BC=bcm,其它条件不变,你能猜出MN的长度吗?请你用一句简洁的话表述你发现的规律.
(3)对于(1)题,如果我们这样叙述它:“已知线段AC=6cm,BC=4cm,点C在直线AB上,点M,N分别是AC,BC的中点,求MN的长度.”结果会有变化吗?如果有,求出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,∠C=90°,点D,E分别是△ABC边AC,BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在线段AB上,如图①所示,且∠α=50°,则∠1+∠2=________°;
(2)若点P在边AB上运动,如图②所示,则∠α,∠1,∠2之间的关系为:____________;

(3)若点P运动到边AB的延长线上,如图③所示,则∠α,∠1,∠2之间有何关系?猜想并说明理由;

(4)若点P运动到△ABC形外,如图④所示,则∠α,∠1,∠2之间的关系为:____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.小美根据学习函数的经验,对函数
的图象与性质.小美根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小美的探究过程,请补充完整:
的图象与性质进行了探究.下面是小美的探究过程,请补充完整:
(![]() )函数
)函数![]() 的自变量
的自变量![]() 的取值范围是__________.
的取值范围是__________.
(![]() )下表是
)下表是![]() 与
与![]() 的几组对应值.
的几组对应值.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
如图,在平面直角坐标系![]() 中,描出以上表中各对对应值为坐标的点.
中,描出以上表中各对对应值为坐标的点.
根据描出的点,画出该函数的图象,标出函数的解析式.

(![]() )结合函数的图象,写出该函数的一条性质:__________.
)结合函数的图象,写出该函数的一条性质:__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com