


科目:初中数学 来源: 题型:
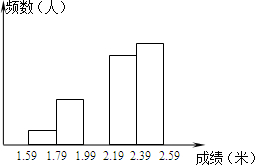 (2013•湖州一模)为增强学生的身体素质,我校坚持长年的全员体育锻炼,并定期进行体能测试,下图是将初三某班学生的立定跳远成绩(精确到0.1米)进行整理后,画出的频数分布直方图的一部分,已知从左到右第一、二、四、五组的频率分别是0.05,0.15,0.30,0.35,第三小组的频数为9人(共有5个小组).
(2013•湖州一模)为增强学生的身体素质,我校坚持长年的全员体育锻炼,并定期进行体能测试,下图是将初三某班学生的立定跳远成绩(精确到0.1米)进行整理后,画出的频数分布直方图的一部分,已知从左到右第一、二、四、五组的频率分别是0.05,0.15,0.30,0.35,第三小组的频数为9人(共有5个小组).查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com