Question

（本题12分） 如图，等腰梯形ABCD中，AD∥BC，点E是线段AD上的一个动点（E与A、D不重合），G、F、H分别是BE、BC、CE的中点．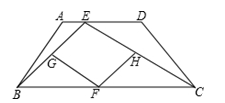

（1）试探索四边形EGFH的形状，并说明理由；
（2）当点E运动到什么位置时，四边形EGFH是菱形？并说明理由；
（3）若（2）中的菱形EGFH是正方形，请探索线段EF与线段BC的关系，并说明你的理由．

Answer 1

（1）EFGH为平行四边形（2）当点E运动到AD的中点时，四边形EGFH是菱形（3）EF⊥BC，EF=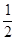BC

解析试题分析：解：（1） EFGH为平行四边形
理由：∵G、F、H分別是BE、BC、CE的中点
∴GF∥EC ，FH∥BE∴ EFGH为平行四边形 ……4分
（2）当点E运动到AD的中点时，四边形EGFH是菱形
理由：∵四边形ABCD是等腰梯形
∴AB="CD" ∠A=∠D
∵AE=DE
∴△ABE≌△DCE
∴BE=CE
∵G、H分別是BE、CE的中点
∴GF=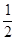BE,FH=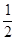CE
∴GF=FH
∵ EFGH为平行四边形
∴四边形EFGH是菱形……4分
（3）EF⊥BC,EF=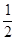BC
理由：∵ 四边形EGFH是正方形
∴EG=EH,∠BEC=90°
∵BE=CE,F为BC的中点，
∴EF⊥BC，EF=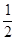BC……4分（答对一半得2分）
考点： 本题考查了多边形的判定
点评：此类试题属于难度一般的试题，考生在解答此类试题时一定要对各多边形的基本判定熟练把握