
| A.一、二、三象限 | B.一、二、四象限 | C.一、三、四象限 | D.二、三、四象限 |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:填空题
 上的一个动点,过点P作PA⊥x轴,垂足为A,请问:y轴上是否存在一点B,使得△PAB为等腰直角三角形。小明发现,点P坐标为(2,2)时,y轴上存在B(0,2),使得△PAB为等腰直角三角形。请写出其它点P的坐标
上的一个动点,过点P作PA⊥x轴,垂足为A,请问:y轴上是否存在一点B,使得△PAB为等腰直角三角形。小明发现,点P坐标为(2,2)时,y轴上存在B(0,2),使得△PAB为等腰直角三角形。请写出其它点P的坐标 
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 是过点(3,0),并且垂直于
是过点(3,0),并且垂直于 轴,从2,3,4,5这四个数中,任取两个数
轴,从2,3,4,5这四个数中,任取两个数 和
和 (
( ),构成函数
),构成函数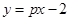 和
和 ,使两个函数图象的交点在直线
,使两个函数图象的交点在直线 的左侧,则这样的有序数组(
的左侧,则这样的有序数组( )共有()
)共有()| A.5组 | B.6组 | C.7组 | D.8组 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题


 (万元)与其销售量x(万盒)之间的函数关系式,并指出x的取值范围;
(万元)与其销售量x(万盒)之间的函数关系式,并指出x的取值范围; (万元)与卖给茶叶经销商的销售量x(万盒)之间的函数关系式,并指出x的取值范围;
(万元)与卖给茶叶经销商的销售量x(万盒)之间的函数关系式,并指出x的取值范围;查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

A. | B. | C. | D. |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 时间(x天) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 售价y(元/件) | 550 | 500 | 450 | 400 | 350 | 300 | 300 | 300 | 300 | 300 |
 (件)与第x天的关系式为
(件)与第x天的关系式为 =20x+40(1≤x≤6且为整数);后4天(7≤x≤10,且为整数)的销售数量
=20x+40(1≤x≤6且为整数);后4天(7≤x≤10,且为整数)的销售数量 件与第x天的关系如图所示
件与第x天的关系如图所示 与x之间的一次函数关系式.
与x之间的一次函数关系式.

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (万件)、供应量
(万件)、供应量 (万件)与价格
(万件)与价格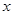 (元/件)分别近似满足下列函数关系式:
(元/件)分别近似满足下列函数关系式: ,
, .需求量为
.需求量为 时,即停止供应.当
时,即停止供应.当 时,该商品的价格称为稳定价格,需求量称为稳定需求量.
时,该商品的价格称为稳定价格,需求量称为稳定需求量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com