
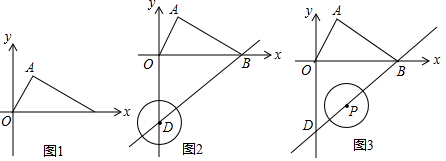
ЗжЮі ЃЈ1ЃЉШчЭМ1жаЃЌзїAHЁЭOBгкHЃЌгЩtanЁЯAOH=$\frac{AH}{OH}$=$\sqrt{3}$ЃЌtanЁЯABH=$\frac{AH}{BH}$=$\frac{\sqrt{3}}{3}$ЃЌЭЦГіЁЯAOH=60ЁуЃЌЁЯABO=30ЁуЃЌМДПЩНтОіЮЪЬтЃЎ
ЃЈ2ЃЉШчЭМ2жаЃЌЙ§ЕуBзїBM1ЁЭxжсНЛOAЕФбгГЄЯпгкM1ЃЌдкBM1ШЁвЛЕуM2ЪЙЕУЁЯM2OB=30ЁуЃЌзїBM3ЁЭOM2гкM3ЃЌдђЁїOBM1ЃЌЁїOBM2ЃЌЁїOBM3ЖМгыЁїOABЯрЫЦЃЎЗжБ№ЧѓГіЕуMЕФзјБъМДПЩЃЎ
ЃЈ3ЃЉЂйШчЭМ3жаЃЌзїDMЁЭAЁфBЁфгкMЃЌOЁфBЁфгыODНЛгкЕуNЃЌИљОнDMЃМ1ЃЌDNЃМ1ПЩЕУвд1ЮЊАыОЖЕФЁбDгыOЁфBЁфгаСНИіНЛЕуЃЌгыAЁфBЁфгаСНИіНЛЕуЃЈBЁфЕужиИДЃЉЃЌгЩДЫМДПЩНтОіЮЪЬтЃЎЂкЧѓГіСНжжЬиЪтЮЛжУЪБtЕФжЕЃЌaЁЂЕБЁбPгыxжсЯрЧаЪБЃЌзїPMЁЭOBгкMЃЌдђPM=0.5tЃЌгЩPMЁЮODЃЌDP=tЃЌPB=5-tЃЌЕУ$\frac{PM}{OD}$=$\frac{BP}{BD}$ЃЌСаГіЗНГЬЧѓГіtЃЎbЁЂЕБЁбPЁфЕФдВаФPЁфдкxЩЯЗНЪБЃЌОЙ§ЕуBЃЌдђгаt-5=0.5tЃЌЧѓГіtЃЌгЩДЫМДПЩНтОіЮЪЬтЃЎ
НтД№ НтЃКЃЈ1ЃЉШчЭМ1жаЃЌзїAHЁЭOBгкHЃЌ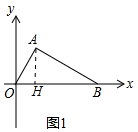
ЁпAЃЈ1ЃЌ$\sqrt{3}$ЃЉЃЌBЃЈ4ЃЌ0ЃЉЃЎ
ЁрOH=1ЃЌAH=$\sqrt{3}$ЃЌBH=3ЃЌ
ЁрtanЁЯAOH=$\frac{AH}{OH}$=$\sqrt{3}$ЃЌtanЁЯABH=$\frac{AH}{BH}$=$\frac{\sqrt{3}}{3}$ЃЌ
ЁрЁЯAOH=60ЁуЃЌЁЯABO=30ЁуЃЌ
ЁрЁЯOAB=180Ёу-ЁЯAOB-ЁЯABO=90ЁуЃЌ
ЁрOAЁЭABЃЎ
ЃЈ2ЃЉШчЭМ2жаЃЌЙ§ЕуBзїBM1ЁЭxжсНЛOAЕФбгГЄЯпгкM1ЃЌдкBM1ШЁвЛЕуM2ЪЙЕУЁЯM2OB=30ЁуЃЌзїBM3ЁЭOM2гкM3ЃЌдђЁїOBM1ЃЌЁїOBM2ЃЌЁїOBM3ЖМгыЁїOABЯрЫЦЃЎ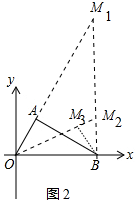
дкRtЁїOBM1жаЃЌЁпOB=4ЃЌЁЯBOM1=60ЁуЃЌ
ЁрBM1=$\sqrt{3}$BO=4$\sqrt{3}$ЃЌ
ЁрM1ЃЈ4ЃЌ4$\sqrt{3}$ЃЉЃЎ
дкRtЁїOBM2жаЃЌЁпOB=4ЃЌЁЯM2OB=30ЁуЃЌ
ЁрBM2=$\frac{\sqrt{3}}{3}$OB=$\frac{4\sqrt{3}}{3}$ЃЌ
ЁрM2ЃЈ4ЃЌ$\frac{4\sqrt{3}}{3}$ЃЉЃЎ
дкRtЁїOBM3жаЃЌЁпЁЯM3OB=30ЁуЃЌЁЯOM3B=90ЁуЃЌ
ЁрOM3=$\frac{\sqrt{3}}{2}$OB=2$\sqrt{3}$ЃЌПЩЕУM3ЃЈ3ЃЌ$\sqrt{3}$ЃЉЃЎ
злЩЯЫљЪіЃЌЕуMЕФзјБъЮЊЃЈ4ЃЌ4$\sqrt{3}$ЃЉЛђЃЈ4ЃЌ$\frac{4\sqrt{3}}{3}$ЃЉЛђЃЈ3ЃЌ$\sqrt{3}$ЃЉ
ЃЈ3ЃЉЂйШчЭМ3жаЃЌзїDMЁЭAЁфBЁфгкMЃЌOЁфBЁфгыODНЛгкЕуNЃЌ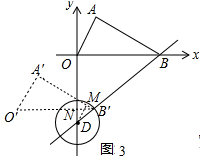
гЩЬтвтBBЁф=4ЃЌ
ЁпOB=4ЃЌOD=3ЃЌЁЯBOD=90ЁуЃЌ
ЁрBD=$\sqrt{O{B}^{2}+O{D}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5ЃЌ
ЁрDBЁф=1ЃЌ
ЁрDMЃМDBЁфЃЌDNЃМDBЁфМДDMЃМ1ЃЌDNЃМ1
Ёрвд1ЮЊАыОЖЕФЁбDгыOЁфBЁфгаСНИіНЛЕуЃЌгыAЁфBЁфгаСНИіНЛЕуЃЈBЁфЕужиИДЃЉЃЌ
ЁрЁїAOBгывдDЮЊдВаФЃЌвд1ЮЊАыОЖЕФЁбDЕФЙЋЙВЕуЕФИіЪ§ЮЊ3ИіЃЎ
ЂкШчЭМ4жаЃЌ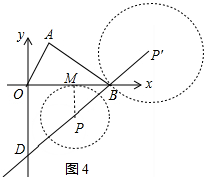
aЁЂЕБЁбPгыxжсЯрЧаЪБЃЌзїPMЁЭOBгкMЃЌдђPM=0.5tЃЌ
ЁпPMЁЮODЃЌDP=tЃЌPB=5-tЃЌ
Ёр$\frac{PM}{OD}$=$\frac{BP}{BD}$ЃЌ
Ёр$\frac{0.5t}{3}$=$\frac{5-t}{5}$ЃЌ
Ёрt=$\frac{30}{11}$УыЃЎ
bЁЂЕБЁбPЁфЕФдВаФPЁфдкxЩЯЗНЪБЃЌОЙ§ЕуBЃЌдђгаt-5=0.5tЃЌ
Ёрt=10ЃЌ
злЩЯЫљЪіЃЌЕБ$\frac{30}{11}$ЁмtЁм10ЪБЃЌPЮЊдВаФЃЌвд0.5tЮЊАыОЖЕФЁбPгыЁїAOBгаЙЋЙВЕуЃЎ
ЕуЦР БОЬтПМВщдВзлКЯЬтЁЂШёНЧШ§НЧКЏЪ§ЁЂЯрЫЦШ§НЧаЮЕФХаЖЈКЭаджЪЁЂжБЯпгыдВЕФЮЛжУЙиЯЕЁЂЙДЙЩЖЈРэЕШжЊЪЖЃЌНтЬтЕФЙиМќЪЧбЇЛсЗжРрЬжТлЕФЫМЯыЫМПМЮЪЬтЃЌбЇЛсРћгУЬиЪтЮЛжУНтОіЮЪЬтЃЌЪєгкжаПМбЙжсЬтЃЎ


 БЖЫйбЕСЗЗЈжБЭЈжаПМПМЕуЯЕСаД№АИ
БЖЫйбЕСЗЗЈжБЭЈжаПМПМЕуЯЕСаД№АИ вЛОэИуЖЈЯЕСаД№АИ
вЛОэИуЖЈЯЕСаД№АИ УћаЃзївЕБОЯЕСаД№АИ
УћаЃзївЕБОЯЕСаД№АИ ЧсЧЩЖсЙкжмВтдТПМжБЭЈУћаЃЯЕСаД№АИ
ЧсЧЩЖсЙкжмВтдТПМжБЭЈУћаЃЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
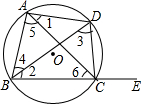 ШчЭМЃЌЫФБпаЮABCDФкНггкЁбOЃЌEЪЧBCбгГЄЯпЩЯвЛЕуЃЌЯТСаЕШЪНжаВЛвЛЖЈГЩСЂЕФЪЧЃЈЁЁЁЁЃЉ
ШчЭМЃЌЫФБпаЮABCDФкНггкЁбOЃЌEЪЧBCбгГЄЯпЩЯвЛЕуЃЌЯТСаЕШЪНжаВЛвЛЖЈГЩСЂЕФЪЧЃЈЁЁЁЁЃЉ| AЃЎ | ЁЯ1=ЁЯ2 | BЃЎ | ЁЯ3=ЁЯ5 | CЃЎ | ЁЯBAD=ЁЯDCE | DЃЎ | ЁЯ4=ЁЯ6 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 180Ёу | BЃЎ | 360Ёу | CЃЎ | 1800Ёу | DЃЎ | ЮоЗЈМЦЫу |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
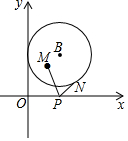 ШчЭМЃЌЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЕуMЃЈ2ЃЌ3ЃЉЁЂвдЕуBЃЈ3ЃЌ4ЃЉЮЊдВаФЃЌ3ЮЊАыОЖзїЁбBЃЌNЪЧЁбBЩЯЕФЖЏЕуЃЌPЮЊxжсЩЯЕФЖЏЕуЃЌдђPM+PNЕФзюаЁжЕЮЊ5$\sqrt{2}$-3ЃЎ
ШчЭМЃЌЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЕуMЃЈ2ЃЌ3ЃЉЁЂвдЕуBЃЈ3ЃЌ4ЃЉЮЊдВаФЃЌ3ЮЊАыОЖзїЁбBЃЌNЪЧЁбBЩЯЕФЖЏЕуЃЌPЮЊxжсЩЯЕФЖЏЕуЃЌдђPM+PNЕФзюаЁжЕЮЊ5$\sqrt{2}$-3ЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
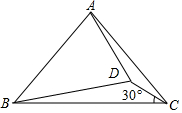 ШчЭМЃЌдкЁїABCжаЃЌAB=ACЃЌНёдкЁїABCФкВПШЁвЛЕуDЪЙЕУAB=BD=ACЧвЁЯDCB=30ЁуЃЌШєCD=2ЧвAC=2$\sqrt{37}$ЃЌЪдЧѓЁїABCУцЛ§ЃЈЧыЯъЪіРэгЩЃЉЃЎ
ШчЭМЃЌдкЁїABCжаЃЌAB=ACЃЌНёдкЁїABCФкВПШЁвЛЕуDЪЙЕУAB=BD=ACЧвЁЯDCB=30ЁуЃЌШєCD=2ЧвAC=2$\sqrt{37}$ЃЌЪдЧѓЁїABCУцЛ§ЃЈЧыЯъЪіРэгЩЃЉЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com