
����Ŀ����ͼ����P������AB���Ϸ����ҡ�PAB=45�㣬PA=2����M������AB�ϵĶ��㣨��M�����A�غϣ����ֽ���P�Ƶ�A��˳ʱ�뷽����ת60�㣬����Q������M�Ƶ�P����ʱ�뷽����ת60�㵽��N������AQ��PM��PN����ֱ��QN�� 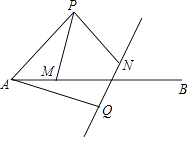
��1����֤��AM=QN��
��2��ֱ��QN���Ե�PΪԲ�ģ���PN�ij�Ϊ�뾶��Բ�Ƿ�������е�����������ڣ��������ʱAM�ij����������ڣ���˵�����ɣ�
��3�����Ե�PΪԲ�ģ���PN�ij�Ϊ�뾶��Բ������Qʱ��ֱ��д���ӻ�NQ�������뾶��Χ�ɵ����ε������
���𰸡�
��1��֤������ͼ1������PQ��
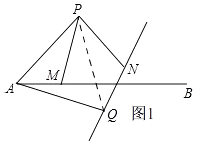
�ɵ�P�Ƶ�A��˳ʱ�뷽����ת60�㵽��Q��
�ɵã�AP=AQ����PAQ=60�㣬
���APQΪ�ȱ������Σ�
��PA=PQ����APQ=60�㣬
�ɵ�M�Ƶ�P����ʱ�뷽����ת60�㵽��N��
�ɵã�PM=PN����MPN=60�㣬
���APM=��QPN��
���APM�ա�QPN��SAS����
��AM=QN
��2���⣺���ڣ�
��ͼ2��
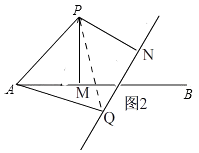
�ɣ�1���е�֤����֪����APM�ա�QPN��
���AMP=��QNP��
��ֱ��QN���Ե�PΪԲ�ģ���PN�ij�Ϊ�뾶��Բ���У�
���AMP=��QNP=90�㣬
����PN��QN��
��R��APM�У���PAB=45�㣬PA=2��
��AM= ![]()
��3���⣺��ͼ3��
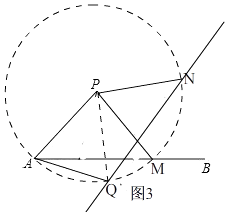
�ɣ�1��֪����APQ�ǵȱ������Σ�
��PA=PQ����APQ=60�㣬
���Ե�PΪԲ�ģ���PN�ij�Ϊ�뾶��Բ������Q��
��PN=PQ=PA��
��PM=PN��
��PA=PM��
�ߡ�PAB=45�㣬
���APM=90�㣬
���MPQ=��APM����APQ=30�㣬
�ߡ�MPN=60�㣬
���QPN=90�㣬
���ӻ�NQ�������뾶��Χ�ɵ����ε����������QPN��������������ε�Բ�Ľǡ�QPN=90�㣬�뾶ΪPN=PM=PA=2��
���ӻ�NQ�������뾶��Χ�ɵ����ε����= ![]() =�У�
=�У�
����������1��������ת����ת�жϳ���APQΪ�ȱ������Σ����жϳ���APM=��QPN���Ӷ��ó���APM�ա�QPN���ɣ���2����ֱ�ߺ�Բ���еó���AMP=��QNP=90�㣬���ù��ɶ�������������ۣ���3�����жϳ�PA=PQ�����жϳ�PQ=PN=PM�����������QPM=30�㣬���������QPN=90�㣬��������ε������ʽ���ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ţ�2��������ίԱ�û��Ƿ�ͳ�Ʊ���40��ͬѧͶ��ʵ����ijɼ��������ͼ��ʾ������40��ͬѧͶ��ʵ����ijɼ�����������λ���ֱ��ǣ� ��
�ɼ� | 6 | 7 | 8 | 9 | 10 |
���� |
| �� | �� | �� | �� |
A.8��8
B.8��8.5
C.9��8
D.9��8.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���B=45�㣬��ACB=30�㣬��D��BC��һ�㣬����AD������A��AG��AD����F���߶�AG�ϣ��ӳ�DA����E��ʹAE=AF������EG��CG��DF����EG=DF����G��AC�Ĵ�ֱƽ�����ϣ��� ![]() ��ֵΪ
��ֵΪ 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijƬ���й���80�ã���������һЩ������߹������������������������ô��֮��ľ����ÿ�������ܹ��վͻ���٣��������IJ�����֮���ͣ����ù�ÿ�ù�������y��ǧ�ˣ������ֹ���x���ã�������֮��ĺ�����ϵ��ͼ��ʾ�� 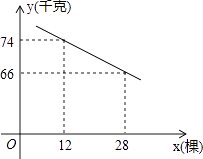
��1����y��x֮��ĺ�����ϵʽ��
��2����Ͷ��ɱ���͵�����£����ֹ������ٿ�ʱ���������ջ��ʵ6750ǧ�ˣ�
��3�������ֹ������ٿ�ʱ�������ܲ���w��ǧ�ˣ�����������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ԡ�ABCֽƬ�������²����� ��1�β���������ABC���Ź�AB�е�D1��ֱ���۵���ʹ��A����BC���ϵ�A1�����ۺ�D1E1��BC�ľ������h1 �� Ȼ��ԭֽƬ��
��2�β���������AD1E1���Ź�AD1�е�D2��ֱ���۵���ʹ��A����D1E1���ϵ�A1�����ۺ�D1E1��BC�ľ������h2 �� Ȼ��ԭֽƬ��
��
�������������ϲ�����ȥ����������n�β�����õ����ۺ�DnEn��BC�ľ������hn �� ��h=1����hn��ֵ�������ǣ� ��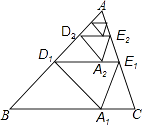
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһƽ��ֱ������ϵ�У�����y=mx+m��y= ![]() ��m��0����ͼ������ǣ� ��
��m��0����ͼ������ǣ� ��
A.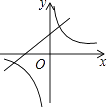
B.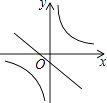
C.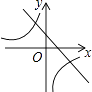
D.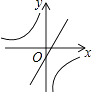
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������죬�����ͬѧ��ְ�������ϼ�̽��үү���̣��ְ�8��30�����г����ߣ�ƽ��ÿСʱ����20km�������ͬѧ������9��30�˹��������У�������ƽ���ٶ���40km/h���ְֵ�����·���������ͬѧ������ij˳�·����ͬ��·�̾�Ϊ40km����ְ�����ʱ��Ϊx��h����
��1����ֱ�д���ְֵ�����·��y1��km���������ͬѧ������ij˳�·��y2��km����x��h��֮��ĺ�������ʽ����ע���Ա�����ȡֵ��Χ��
��2������ͬһ��ƽ��ֱ������ϵ�л�����1��������������ͼ��
��3����ش�˭�ȵ����ϼң�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ҫ�ڿ�Ϊ36m�Ĺ�·���̻���MN����Ϊ4m�������밲װ·�ƣ�·�ƵĵƱ�AD�ij�Ϊ3m���������CD��120�㣨��ͼ��ʾ����·�Ʋ���Բ�ε��֣����ֵ�����AB��Ʊ۴�ֱ�������ֵ�����ͨ����··��һ����м�ʱ����ȥ�̻�����·�沿�֣�������Ч�������룬�ʣ�Ӧ��ƶ�ߵĵ���������ȡ�������������Ч��������ȷ��0.01m���ο����� ![]() ��1.732��
��1.732�� 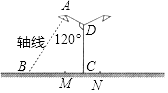
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=4��AD=5��AD��AB��BC�ֱ����O������E��F��G���㣬����D����O������BC�ڵ�M���е�ΪN����DM�ij�Ϊ��������
A.![]()
B.![]()
C.![]()
D.2![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com