
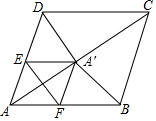
 在菱形ABCD中,AB=5,AC=8,点P是对角线AC上的一个动点,过点P作EF垂直于AC交AD于点E,交AB于点F,将△AEF折叠,使点A落在点A′处,当△A′CD时等腰三角形时,AP的长为$\frac{3}{2}$或$\frac{39}{16}$.
在菱形ABCD中,AB=5,AC=8,点P是对角线AC上的一个动点,过点P作EF垂直于AC交AD于点E,交AB于点F,将△AEF折叠,使点A落在点A′处,当△A′CD时等腰三角形时,AP的长为$\frac{3}{2}$或$\frac{39}{16}$. 分析 首先证明四边形AEA′F是菱形,分两种情形:①CA′=CD,②A′C=A′D分别计算即可.
解答 解:∵四边形ABCD是菱形,
∴AB=BC=CD=AD=5,∠DAC=∠BAC,
∵EF⊥AA′,
∴∠EPA=∠FPA=90°,
∴∠EAP+∠AEP=90°,∠FAP+∠AFP=90°,
∴∠AEP=∠AFP,
∴AE=AF,
∵△A′EF是由△AEF翻折,
∴AE=EA′,AF=FA′,
∴AE=EA′=A′F=FA,
∴四边形AEA′F是菱形,
∴AP=PA′
①当CD=CA′时,∵AA′=AC-CA′=3,
∴AP=$\frac{1}{2}$AA′=$\frac{3}{2}$.
②当A′C=A′D时,∵∠A′CD=∠A′DC=∠DAC,
∴△A′CD∽△DAC,
∴$\frac{A′C}{AD}$=$\frac{DC}{AC}$,
∴A′C=$\frac{25}{8}$,
∴AA=8-$\frac{25}{8}$=$\frac{39}{8}$,
∴AP=$\frac{1}{2}$AA′=$\frac{39}{16}$.
故答案为$\frac{3}{2}$或$\frac{39}{16}$.
点评 本题考查菱形的性质、翻折变换、等腰三角形的判定和性质等知识,解题的关键是学会分类讨论,不能漏解,属于中考常考题型.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{x}-\frac{1}{y}=\frac{x-y}{xy}$ | B. | $\frac{b}{a-b}$+$\frac{a}{b-a}$=-1 | C. | $\frac{-a-1}{{{a^2}-1}}=-\frac{1}{a+1}$ | D. | $\frac{{{a^2}-1}}{a}•\frac{1}{a+1}=-1$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=4$\sqrt{3}$,则圆锥底面圆的半径是( )
如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=4$\sqrt{3}$,则圆锥底面圆的半径是( )| A. | $\frac{4}{3}$ | B. | $\frac{2}{3}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
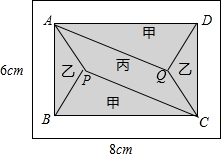 小黄准备给长8m,宽6m的长方形客厅铺设瓷砖,现将其划分成一个长方形ABCD区域Ⅰ(阴影部分)和一个环形区域Ⅱ(空白部分),其中区域Ⅰ用甲、乙、丙三种瓷砖铺设,且满足PQ∥AD,如图所示.
小黄准备给长8m,宽6m的长方形客厅铺设瓷砖,现将其划分成一个长方形ABCD区域Ⅰ(阴影部分)和一个环形区域Ⅱ(空白部分),其中区域Ⅰ用甲、乙、丙三种瓷砖铺设,且满足PQ∥AD,如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com