Question

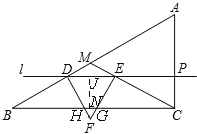
【题目】如图，Rt△ABC中，M为斜边AB上一点，且MB=MC=AC=8cm，平行于BC的直线l从BC的位置出发以每秒1cm的速度向上平移，运动到经过点M时停止. 直线l分别交线段MB、MC、AC于点D、E、P，以DE为边向下作等边△DEF，设△DEF与△MBC重叠部分的面积为S（cm2），直线l的运动时间为t（秒）．

（1）求边BC的长度；

（2）求S与t的函数关系式；

（3）在整个运动过程中，是否存在这样的时刻t，使得以P、C、F为顶点的三角形为等腰三角形？若存在，请求出t的值；若不存在，请说明理由．

（4）在整个运动过程中，是否存在这样的时刻t，使得以点D为圆心、BD为半径的圆与直线EF相切？若存在，请求出t的值；若不存在，请说明理由．

Answer 1

【答案】（1） 8；（2） 当0＜t≤3时，S=﹣t2+8t;当3＜t≤4时，S= 3t2﹣24t+48．（3） t=（4） t=．

【解析】

试题分析：（1）利用直角三角形的性质和锐角三角函数即可；

（2）分两段求出函数关系即可；

（3）进行分类讨论即可求出t的值；

（4）若相切，利用点到圆心的距离等于半径列出方程即可.

试题解析：（1）∵M为斜边中点，

∴∠B=MCB=α，

∴∠AMC=2α，

∵MC=MA，

∴∠A=∠AMC=2α，

∴∠B+∠A=90°，

∴α+2α=90°，

∴α=30°，

∴∠B=30°，

∵cotB=，

∴BC=AC×cotB=8；

（2）由题意，若点F恰好落在BC上，

∴MF=4（4﹣t）=4，

∴t=3．

当0＜t≤3时，如图，

∴BD=2t，DM=8﹣2t，

∵l∥BC，

∴，

∴，

∴DE=（8﹣2t）．

∴点D到EF的距离为FJ=DE=3（4﹣t），

∵l∥BC，

∴，

∵FN=FJ﹣JN=3（4﹣t）﹣t=12﹣4t，

∴HG=（3﹣t）

S=S梯形DHGE=（HG+DE）×FN=﹣t2+8t

当3＜t≤4时，重叠部分就是△DEF，

S=S△DEF=DE2=3t2﹣24t+48．

（3）当0＜t≤3时，∠FCP≥90°，

∴FC＞CP，

∴△PCF不可能为等腰三角形

当3＜t≤4时，若△PCF为等腰三角形，

∴只能FC=FP，

∴=3（4﹣t），

∴t=

（4）若相切，

∵∠B=30°，

∴BD=2t，DM=8﹣2t，

∵l∥BC，

∴，

∴，

∴DE=（8﹣2t）．

∴点D到EF的距离为DE=3（4﹣t）

∴2t=3（4﹣t），

解得t=．