
| H | G | |
| 价格(万元/台) | 15 | 12 |
| 处理污水量(吨/月) | 250 | 220 |
 ,
,

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:解答题
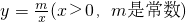 的图象经过A(1,4),B(a,b),其中a>
的图象经过A(1,4),B(a,b),其中a> 1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.
1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 甲=1.5,甲的样本方差为s甲2=1.65,请你计算乙的样本平均数
甲=1.5,甲的样本方差为s甲2=1.65,请你计算乙的样本平均数 乙=________,若乙的样本方差s乙2=0.76,则估计________机床的性能较好.
乙=________,若乙的样本方差s乙2=0.76,则估计________机床的性能较好.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com