
【题目】在ABCD中,过点D作DE⊥AB于点E,点F 在边CD上,DF=BE,连接AF,BF. 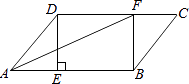
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD.
∵BE∥DF,BE=DF,
∴四边形BFDE是平行四边形.
∵DE⊥AB,
∴∠DEB=90°,
∴四边形BFDE是矩形
(2)解:∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠DFA=∠FAB.
在Rt△BCF中,由勾股定理,得
BC= ![]() =
= ![]() =5,
=5,
∴AD=BC=DF=5,
∴∠DAF=∠DFA,
∴∠DAF=∠FAB,
即AF平分∠DAB.
【解析】(1)根据平行四边形的性质,可得AB与CD的关系,根据平行四边形的判定,可得BFDE是平行四边形,再根据矩形的判定,可得答案;(2)根据平行线的性质,可得∠DFA=∠FAB,根据等腰三角形的判定与性质,可得∠DAF=∠DFA,根据角平分线的判定,可得答案.


科目:初中数学 来源: 题型:
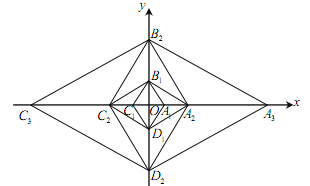
【题目】(成都)已知菱形![]() 的边长为2,
的边长为2,![]() =60°,对角线
=60°,对角线![]() ,
,![]() 相交于点O.以点O为坐标原点,分别以
相交于点O.以点O为坐标原点,分别以![]() ,
,![]() 所在直线为x轴、y轴,建立如图所示的直角坐标系.以
所在直线为x轴、y轴,建立如图所示的直角坐标系.以![]() 为对角线作菱形
为对角线作菱形![]() ∽菱形
∽菱形![]() ,再以
,再以![]() 为对角线作菱形
为对角线作菱形![]() ∽菱形
∽菱形![]() ,再以
,再以![]() 为对角线作菱形
为对角线作菱形![]() ∽菱形
∽菱形![]() ,,按此规律继续作下去,在x轴的正半轴上得到点
,,按此规律继续作下去,在x轴的正半轴上得到点![]() ,
,![]() ,
,![]() ,......,
,......,![]() ,则点
,则点![]() 的坐标为________.
的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD相交于点O,AE=CF. 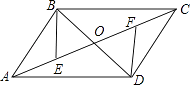
(1)求证:△BOE≌△DOF;
(2)连接DE、BF,若BD⊥EF,试探究四边形EBDF的形状,并对结论给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
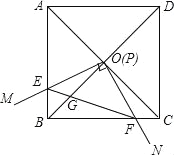
【题目】如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是 .
(1)EF=![]() OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)BE+BF=
OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)BE+BF=![]() OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=
OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=![]() ;(5)OGBD=AE2+CF2.
;(5)OGBD=AE2+CF2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽上午9:00从家里出发,骑车去一家超市购物,然后从这家超市返回家中,小丽离家的距离y(米)和所经过的时间x(分)之间的函数关系图象如图所示.请根据图象回答下列问题: 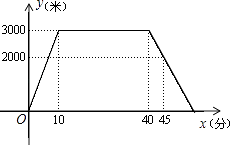
(1)小丽去超市途中的速度是米/分;在超市逗留了分;
(2)求小丽从超市返回家中所需要的时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
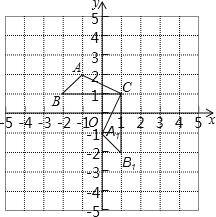
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(﹣1,2)、B(﹣2,1)、C(1,1)(正方形网格中每个小正方形的边长是1个单位长度).
(1)△A1B1C1是△ABC绕点 逆时针旋转 度得到的,B1的坐标是 ;
(2)求出线段AC旋转过程中所扫过的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是 ( )
A. 一个数的平方根有两个,它们互为相反数 . B. 一个数的立方根不是正数就是负数
C. 负数没有立方根 D. 如果一个数的立方根是这个数本身,那么这个数一定是-1或0或1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com