练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知：a为有理数，a3+a2+a+1=0，求1+a+a2+a3+…+a2012的值．

     

    【答案】

    1

    【解析】

    试题分析：首先将1+a+a2+a3+…+a2012变形为：1+a（a+a2+a3）+a5（1+a+a2+a3）…+a2009（1+a+a2+a3），然后将a3+a2+a+1=0代入即可求得答案．

    解：∵a3+a2+a+1=0，

    ∴1+a+a2+a3+…+a2012，

    =1+a（1+a+a2+a3）+a5（1+a+a2+a3）…+a2009（1+a+a2+a3），

    =1．

    考点：因式分解的应用．

    点评：此题考查了因式分解的应用．得到1+a（a+a2+a3）+a5（1+a+a2+a3）…+a2009（1+a+a2+a3）是解此题的关键．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    33、已知：a为有理数，a3+a2+a+1=0，求1+a+a2+a3+…+a2012的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    下面是按一定规律排列的一列数：

    　　　 第1个数：；

    　　　 第2个数：；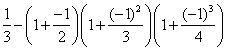

    　　　 第3个数：；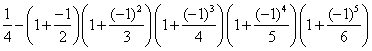

    　　　 ……

    　　　 第个数：．

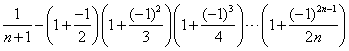    　　　 那么，在第10个数、第11个数、第12个数、第13个数中，最大的数是（）

    　　A．第10个数 　　　B．第11个数　　　C．第12个数　　　D．第13个数

    　　3．已知：a为有理数，a3+a2+a+1=0，求1+a+a2+a3+…+a2012的值．

    　　4．已知：，，求ab的值。

    　　5．当整数k为何值时，方程9x-3=kx+14有正整数解？并求出正整数解

     

    查看答案和解析>>

    科目：初中数学 来源：2013年初中数学单元提优测试卷-因式分解的应用（带解析） 题型：解答题

    已知：a为有理数，a3+a2+a+1=0，求1+a+a2+a3+…+a2012的值．

    查看答案和解析>>

    科目：初中数学 来源：2011年江苏省镇江丹徒区初一上学期期末数学卷 题型：解答题

    下面是按一定规律排列的一列数：

    　　　 第1个数：；

    　　　 第2个数：；

    　　　 第3个数：；

    　　　 ……

    　　　 第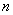个数：．

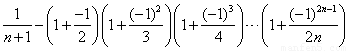    　　　 那么，在第10个数、第11个数、第12个数、第13个数中，最大的数是（ ）

    　　A．第10个数 　　　B．第11个数 　　　C．第12个数　　　 D．第13个数

    　　3．已知：a为有理数，a3+a2+a+1=0，求1+a+a2+a3+…+a2012的值．

    　　4．已知：，，求ab的值。

    　　5．当整数k为何值时，方程9x-3=kx+14有正整数解？并求出正整数解

     

    查看答案和解析>>

    同步练习册答案