
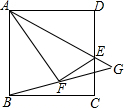
 如图,正方形ABCD中,E是CD的中点,连接AE,沿AE折叠,使得点D落在正方形内的点F处,连接BF并延长,交AE的延长线于点G.
如图,正方形ABCD中,E是CD的中点,连接AE,沿AE折叠,使得点D落在正方形内的点F处,连接BF并延长,交AE的延长线于点G.分析 (1)过F作BC的平行线,交AB于H,交CD于P,构造相似三角形,设DE=1=FE,EP=x,求得FH=2x,依据在Rt△AHF中,AH2+HF2=AF2,即可得到x=$\frac{3}{5}$,根据HF=$\frac{6}{5}$,HB=AB-AH=$\frac{2}{5}$,即可得出tan∠CBG=tan∠BFH=$\frac{BH}{FH}$=$\frac{1}{3}$;
(2)连接DF交AG于O,则DF⊥AG,得到FO=$\frac{AF×EF}{AG}$=$\frac{2}{5}\sqrt{5}$,根据tan∠CBG=$\frac{1}{3}$,得到EQ=1-$\frac{2}{3}$=$\frac{1}{3}$,再根据△GEQ∽△GAB,得出$\frac{GE}{GA}=\frac{EQ}{AB}$,求得GE=$\frac{\sqrt{5}}{5}$,根据△EGF的面积=$\frac{1}{2}$GE×FO进行计算即可.
解答 解:(1)如图,过F作BC的平行线,交AB于H,交CD于P,则HP与AB、CD都垂直,
设DE=1=FE,EP=x,则正方形的边长为2,DP=1+x=AH,
由折叠可得,AF=AD=2,∠AFE=∠ADE=90°,
∴∠FAH=∠EFP,
∴△FAH∽△EFP,
∴$\frac{HF}{PE}=\frac{AF}{FE}$,即$\frac{FH}{x}=\frac{2}{1}$,
∴FH=2x,
在Rt△AHF中,AH2+HF2=AF2,
∴(1+x)2+(2x)2=22,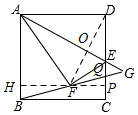
解得x=$\frac{3}{5}$,(负值已舍去)
∴HF=$\frac{6}{5}$,HB=AB-AH=$\frac{2}{5}$,
∴tan∠CBG=tan∠BFH=$\frac{BH}{FH}$=$\frac{1}{3}$;
(2)如图,连接DF交AG于O,则DF⊥AG,
∵AB=2,
∴AF=2,EF=1,AE=$\sqrt{5}$
∴FO=$\frac{AF×EF}{AG}$=$\frac{2}{5}\sqrt{5}$,
∵tan∠CBG=$\frac{1}{3}$,
∴$\frac{CQ}{BC}$=$\frac{1}{3}$,即CQ=$\frac{1}{3}$BC=$\frac{2}{3}$,
∴EQ=1-$\frac{2}{3}$=$\frac{1}{3}$,
∵EQ∥AB,
∴△GEQ∽△GAB,
∴$\frac{GE}{GA}=\frac{EQ}{AB}$,即$\frac{GE}{GE+\sqrt{5}}=\frac{\frac{1}{3}}{2}$,
解得GE=$\frac{\sqrt{5}}{5}$,
∴△EGF的面积=$\frac{1}{2}$GE×FO=$\frac{1}{2}$×$\frac{\sqrt{5}}{5}$×$\frac{2}{5}\sqrt{5}$=$\frac{1}{5}$.
点评 本题主要考查了折叠问题,正方形的性质,解直角三角形,勾股定理以及相似三角形的判定与性质的综合应用,解决问题的关键是作辅助线构造相似三角形,依据相似三角形的对应边成比例列式计算.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
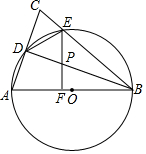 已知:如图,在△ABC中,AB=BC=10,以AB为直径作⊙O分别交AC,BC于点D,E,连接DE和DB,过点E作EF⊥AB,垂足为F,交BD于点P.
已知:如图,在△ABC中,AB=BC=10,以AB为直径作⊙O分别交AC,BC于点D,E,连接DE和DB,过点E作EF⊥AB,垂足为F,交BD于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售时段 | 销售数量 | 销售收入 | |
| A种型号 | B种型号 | ||
| 第一天 | 3台 | 5台 | 1800元 |
| 第二天 | 4台 | 10台 | 3100元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明在拼图时,发现8个大小一样的小长方形,如图(1)所示,恰好可以拼成一个大的长方形.小红看见了,说“我来试一试”,结果小红七拼八凑,拼成如图(2)那样的正方形,中间恰好是2mm的小正方形.求图(2)大正方形的面积.
小明在拼图时,发现8个大小一样的小长方形,如图(1)所示,恰好可以拼成一个大的长方形.小红看见了,说“我来试一试”,结果小红七拼八凑,拼成如图(2)那样的正方形,中间恰好是2mm的小正方形.求图(2)大正方形的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
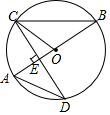 如图,AB是圆O的直径.CD是圆O的一条弦.且CD⊥AB于点E.
如图,AB是圆O的直径.CD是圆O的一条弦.且CD⊥AB于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
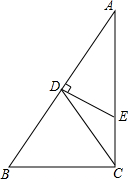 在Rt△ABC中,∠ACB=90°,D为AB边上的中点,DE⊥AB,AD=2DE.
在Rt△ABC中,∠ACB=90°,D为AB边上的中点,DE⊥AB,AD=2DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
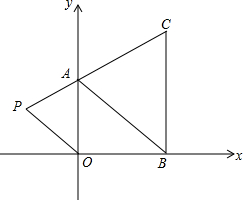 如图,在下面直角坐标系中,已知A(0,2),B(3,0),C(3,4)三点,在第二象限内有一点P(m,$\frac{1}{2}$).
如图,在下面直角坐标系中,已知A(0,2),B(3,0),C(3,4)三点,在第二象限内有一点P(m,$\frac{1}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 8个一样大小的长方形恰好拼成一个大的长方形(如图),若大长方形的宽为12cm,则每一个小长方形的面积为( )
8个一样大小的长方形恰好拼成一个大的长方形(如图),若大长方形的宽为12cm,则每一个小长方形的面积为( )| A. | 12cm2 | B. | 16cm2 | C. | 24cm2 | D. | 27cm2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com