解:(1)依题意得:

,
解得:

,
∴抛物线的解析式为:y=

x
2+
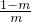
x-1;
(2)∵x=0时,y=-1,
∴C(0,-1),
∵OA=OC,
∴∠OAC=45°,
∴∠BMC=2∠OAC=90°.
又∵
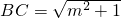
,
∴
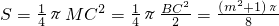
;
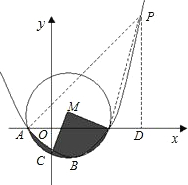
(3)如图,由抛物线的对称性可知,若抛物线上存在点P,使得以A、B、P为顶点的三角形与△ABC相似,
则P关于对称轴的对称点P'也符合题意,即P、P'对应的m值相同.下面以点P在对称轴右侧进行分析:
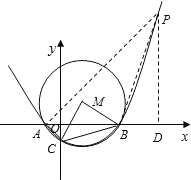
情形一:若△ABC∽△APB,
∴∠PAB=∠BAC=45°,

,
过P作PD⊥x轴垂足为D,连PA、PB.
在Rt△PDA中,∵∠PAB=∠BAC=45°,
∴PD=AD,
∴可令P(x,x+1),
若P在抛物线上,
则有x+1=

x
2+
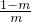
x-1.
即x
2+(1-2m)x-2m=0,
解得x
1=-1,x
2=2m,
∴P
1(2m,2m+1),P
2(-1,0)显然P
2不合题意,舍去.
此时AP=

PD=(2m+1)

;①
又由

,得
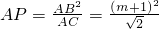
;②
由①、②有:(2m+1)

=
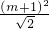
.
整理得:m
2-2m-1=0,
解得:m=1±

,
∵m>0,
∴m=1+

.
即若抛物线上存在点P,使得以A、B、P为顶点的三角形与△ABC相似,
则m=1+

;
情形二:△ABC∽△PAB,
则∠PAB=∠ABC,
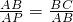
,
同于情形一:∵∠PAB=∠ABC,
∴
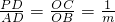
,
∴可令P(x,

(x+1)),
若P在抛物线上,则有

(x+1)=

x
2+
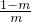
x-1.
整理得:x
2-mx-m-1=0,
解得:x
1=-1,x
2=m+1,
∴P(m+1,

(m+2))或P(-1,0),
显然P(-1,0)不合题意,舍去.
此时
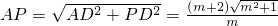
;①
又由
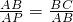
得:
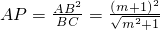
;②
由①、②得:
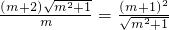
,
整理得m
2=m
2+1,显然无解.
综合情形一二得:若抛物线上存在点P,使得以A、B、P为顶点的三角形与△ABC相似,则m=1+

.
分析:(1)根据所给的A、B的值,代入二次函数,可求出a、b的值,得到二次函数的表达式;
(2)由点的坐标可得到△AOC是等腰直角三角形,从而得到∠CMD=90°,再利用扇形面积公式可计算出面积;
(3)利用三角形的相似,得到比例线段求出m的值,需考虑到有两种情况.
点评:综合考查了用待定系数法求二次函数的解析式,两点之间的距离公式,圆心角等于圆周角的2倍.相似三角形的判定和性质,勾股定理等知识点,具有较强的综合性.

 C.
C. 解:(1)依题意得:
解:(1)依题意得: ,
, ,
, x2+
x2+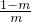 x-1;
x-1;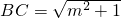 ,
,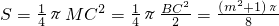 ;
;
 ,
, x2+
x2+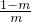 x-1.
x-1. PD=(2m+1)
PD=(2m+1) ;①
;① ,得
,得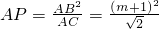 ;②
;② =
=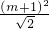 .
. ,
, .
. ;
;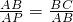 ,
,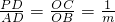 ,
, (x+1)),
(x+1)), (x+1)=
(x+1)= x2+
x2+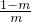 x-1.
x-1. (m+2))或P(-1,0),
(m+2))或P(-1,0),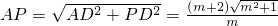 ;①
;①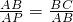 得:
得: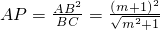 ;②
;②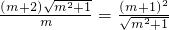 ,
, .
.

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案 与x轴的另一个交点为E.
与x轴的另一个交点为E. 如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=
如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=