

分析 (1)如图1中,作AH⊥BC于H.利用等腰直角三角形的性质求出AH,在Rt△AEH中,根据EH=$\frac{AH}{tan30°}$,求出EH即可解决问题.
(2)如图2中,连接AD.由△BHD∽△CHA,推出△AHD∽△CHB,推出∠ADH=∠CBH=45°,∠DAH=∠BCH,推出∠ADB=90°+45°=135°,推出∠ADE=360°-90°-135°=135°,即∠ADE=∠ADB,推出△ADE≌△ADB,即可解决问题.
解答 (1)解:如图1中,作AH⊥BC于H.
∵AB=AC,∠BAC=90°,AH⊥BC,
∴AH=BH=HC=2,
在Rt△AEH中,∵∠AHE=90°,AH=2,∠AEH=30°,
∴EH=$\frac{AH}{tan30°}$=2$\sqrt{3}$,
∴EB=EH-BH=2$\sqrt{3}$-2.
(2)证明:如图2中,连接AD.
∵∠BDH=∠HAC,∠BHD=∠CHA,
∴△BHD∽△CHA,
∴$\frac{DH}{AH}$=$\frac{BH}{CH}$,
∴$\frac{DH}{BH}$=$\frac{AH}{CH}$,∵∠AHD=∠CHB,
∴△AHD∽△CHB,
∴∠ADH=∠CBH=45°,∠DAH=∠BCH,
∴∠ADB=90°+45°=135°,
∴∠ADE=360°-90°-135°=135°,
∴∠ADE=∠ADB,
在△ADE和△ADB中,
$\left\{\begin{array}{l}{AD=AD}\\{∠ADE=∠ADB}\\{DE=DB}\end{array}\right.$,
∴△ADE≌△ADB,
∴∠DAE=∠DAB,
∵∠DAB=∠BCH,
∴∠EAH=2∠HCB.
点评 本题考查等腰直角三角形的性质、全等三角形的判定和性质、相似三角形的判定和性质、旋转变换、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
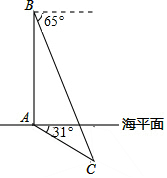 在某次反潜演习中,红方军舰A测得蓝方潜艇C的俯角为31°,位于军舰A正上方800米的红方反潜直升机B测得潜艇C的俯角为65°.试根据以上数据求出潜艇C离开海平面的下潜深度(结果保留整数)
在某次反潜演习中,红方军舰A测得蓝方潜艇C的俯角为31°,位于军舰A正上方800米的红方反潜直升机B测得潜艇C的俯角为65°.试根据以上数据求出潜艇C离开海平面的下潜深度(结果保留整数)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
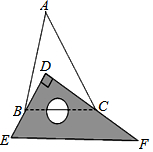 如图,将一块直角三角板DEF放置在锐角△ABC上,使得该三角板的两条直角边DE、DF恰好分别经过点B、C,若∠A=40°,求∠ABD+∠ACD=( )
如图,将一块直角三角板DEF放置在锐角△ABC上,使得该三角板的两条直角边DE、DF恰好分别经过点B、C,若∠A=40°,求∠ABD+∠ACD=( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
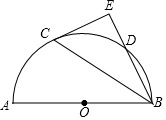 如图,AB为半圆的直径,点C是弧AD的中点,过点C作BD延长线的垂线交于点E.
如图,AB为半圆的直径,点C是弧AD的中点,过点C作BD延长线的垂线交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.1 | B. | 0.15 | C. | 0.25 | D. | 0.3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平均数是15 | B. | 众数是10 | C. | 中位数是17 | D. | 方差是$\frac{44}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com