
【题目】如图,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() .
.

(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() ,
,![]() 的中点,求证:线段
的中点,求证:线段![]() 与线段
与线段![]() 互相平分.
互相平分.
【答案】(1)见解析;(2)见解析
【解析】
(1)过点D作DM∥AC交BC的延长线于点M,由平行四边形的性质易得AC=DM=DB,∠DBC=∠M=∠ACB,由全等三角形判定定理及性质得出结论;
(2)连接EH,FH,FG,EG,E,F,G,H分别是AD,BC,DB,AC的中点,易得四边形HFGE为平行四边形,由平行四边形的性质及(1)结论得□HFGE为菱形,易得EF与GH互相垂直平分.
解:(1)证明:(1)过点D作DM∥AC交BC的延长线于点M,如图1,
∵AD∥CB,
∴四边形ADMC为平行四边形,
∴AC=DM=DB,∠DBC=∠M=∠ACB,
在△ACB和△DBC中,
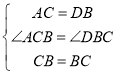 ,
,
∴△ACB≌△DBC(SAS),
∴AB=DC;

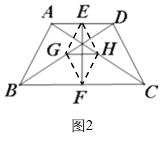
(2)连接EH,FH,FG,EG,如图2,
∵E,F,G,H分别是AD,BC,DB,AC的中点,
∴GE∥AB,且GE=![]() AB,HF∥AB,且HF=
AB,HF∥AB,且HF=![]() AB,
AB,
∴GE∥HF,GE=HF,
∴四边形HFGE为平行四边形,
由(1)知,AB=DC,
∴GE=HE,
∴□HFGE为菱形,
∴EF与GH互相垂直平分.


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCB1中,AB=1,AB与直线l的夹角为30°,延长CB1交直线l于点A1 , 作正方形A1B1C1B2 , 延长C1B2交直线l于点A2 , 作正方形A2B2C2B3 , 延长C2B3交直线l于点A3 , 作正方形A3B3C3B4 , …,依此规律,则A2016A2017= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD与CEFG,如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF的中点H,连接GH.若BC=EF=2,CD=CE=1,则GH=( )

A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人到一家快递公司办理环江香米(简称香米)的快递托运,重量为![]() 千克.快递公司收取托运费方案如下:
千克.快递公司收取托运费方案如下:
凡物品重量不超过10千克的,按2元/千克收取托运费;当物品重量超过10千克的,超出部分按3元/千克加收托运费.
(1)写出![]() 千克香米的托运费的表达式 (用含字母
千克香米的托运费的表达式 (用含字母![]() 的式子表示);
的式子表示);
(2)若托运香米重量为![]() 千克时,求出这笔托运费.
千克时,求出这笔托运费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察图中给出的信息,回答下列问题:
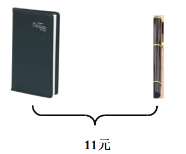

(1)一本笔记本与一支中性笔分别是多少元?
(2)某学校给参加体育比赛获一等奖的10名学生发笔记本,给获二等奖的20名学生发中性笔,现有两个超市在搞促销活动,A超市规定:这两种商品都打八折;B超市规定:每买一个笔记本送一支中性笔,另外购买的中性笔按原价卖.该学校选择哪家超市购买更合算,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教育部明确要求中小学生每天要有2小时体育锻炼,周末朱诺和哥哥在![]() 米的环形跑道上骑车锻炼,他们在同一地点沿着同一方向同时出发,骑行结束后两人有如下对话:
米的环形跑道上骑车锻炼,他们在同一地点沿着同一方向同时出发,骑行结束后两人有如下对话:
朱诺:你要![]() 分钟才能第一次追上我.
分钟才能第一次追上我.
哥哥:我骑完一圈的时候,你才骑了半圈!
(1)请根据他们的对话内容,求出朱诺和哥哥的骑行速度(速度单位:米/秒);
(2)哥哥第一次追上朱诺后,在第二次相遇前,再经过多少秒,朱诺和哥哥相距![]() 米?
米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明:
如图,BE平分∠ABD,DE平分∠BDC,且∠α+∠β=90°,求证:AB∥CD.

证明:∵BE平分∠ABD(已知),∴∠ABD=2∠α( )
∵DE平分∠BDC( )
∴∠BDC= ( ),∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)(等量代换)
∵∠α+∠β=90°(已知),∴∠ABD+∠BDC=( ),∴AB∥CD( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(﹣3,3 ![]() ),反比例函数y=
),反比例函数y= ![]() 的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是 .
的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若(x2+3mx﹣![]() )(x2﹣3x+n)的积中不含x和x3项,
)(x2﹣3x+n)的积中不含x和x3项,
(1)求m2﹣mn+![]() n2的值;
n2的值;
(2)求代数式(﹣18m2n)2+(9mn)﹣2+(3m)2014n2016的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com