
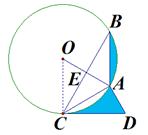
如下图,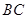 为⊙
为⊙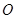 的弦,
的弦,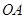 ⊥
⊥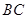 于
于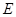 交⊙
交⊙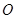 于
于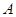 ,
,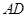 ⊥
⊥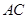 于
于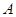 ,∠
,∠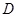 =2∠
=2∠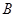 =60o.
=60o.
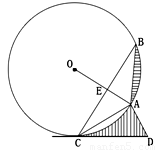
(1)求证,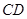 为⊙
为⊙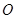 的切线;
的切线;
(2)当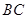 =6时,求阴影部分的面积。
=6时,求阴影部分的面积。
(1)见解析;(2) 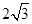
【解析】
试题分析:(1)连接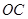 .先根据圆周角定理得到
.先根据圆周角定理得到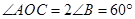 ,即可判断△
,即可判断△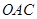 是等边三角形,从而可以判断
是等边三角形,从而可以判断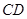 为⊙O的切线;
为⊙O的切线;
(2)先根据垂径定理可得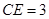 ,
,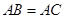 ,再根据含30度角的直角三角形的性质及勾股定理即可求得结果。
,再根据含30度角的直角三角形的性质及勾股定理即可求得结果。
(1)证明:连接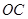 .
.
∵ 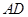 ⊥
⊥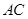 于
于 ,
,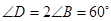 ,
,
∴ 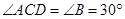 .
.
∴ 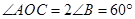 .
.
∵ 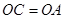 ,
,
∴ △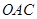 是等边三角形.
是等边三角形.
∴ 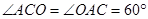 .
.
∴ 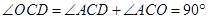 .
.
∵ 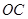 是半径,
是半径,
∴ 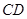 为⊙O的切线
为⊙O的切线
(2)∵ 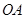 ⊥
⊥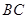 于
于 ,
,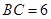 ,
,
∴ 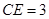 ,
,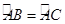 .
.
∴ 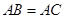 .
.
∵ 在Rt△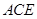 中,
中,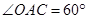 ,
,
∴ 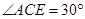 ,
,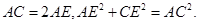
∴  .
.
∵ 在Rt△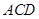 中,
中,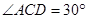 ,
,
∴ 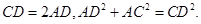
∴ 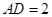 .
.
∴ 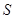 阴影=
阴影=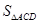 =
= 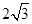 .
.
考点:本题考查的是切线的判定,垂径定理,含30度角的直角三角形的性质及勾股定理
点评:要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2013届福建福州外国语学校九年级上学期期中考试数学试卷(带解析) 题型:解答题
如下图,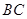 为⊙
为⊙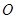 的弦,
的弦,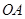 ⊥
⊥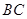 于
于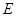 交⊙
交⊙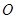 于
于 ,
,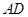 ⊥
⊥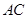 于
于 ,∠
,∠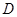 =2∠
=2∠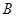 =60o.
=60o.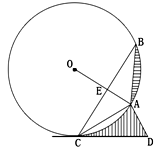
(1)求证,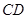 为⊙
为⊙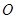 的切线;
的切线;
(2)当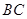 =6时,求阴影部分的面积。
=6时,求阴影部分的面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com