
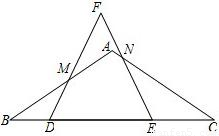
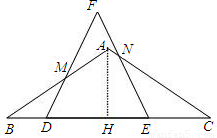
 ,
,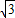 ,AB=
,AB=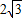 .
. ×6×
×6×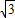 =3
=3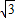 .
. ,
,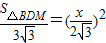 .
.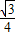 x2同理求得S△NEC=
x2同理求得S△NEC=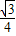 (3-x)2
(3-x)2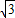 -
-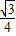 x2-
x2-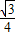 (3-x)2=-
(3-x)2=-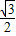 x2+
x2+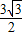 x+
x+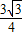 (1≤x≤2).
(1≤x≤2). .
.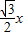 ,BM=
,BM=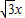 .
.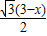 .
.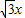 =
=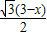 .
.

科目:初中数学 来源: 题型:
 (2009•奉贤区二模)如图,在12×6的网格图中(每个小正方形的边长均为1个单位),圆A的半径为1,圆B的半径为2,要使圆A与静止的圆B内切,那么圆A由图示位置需向右平移
(2009•奉贤区二模)如图,在12×6的网格图中(每个小正方形的边长均为1个单位),圆A的半径为1,圆B的半径为2,要使圆A与静止的圆B内切,那么圆A由图示位置需向右平移查看答案和解析>>
科目:初中数学 来源:2009年上海市奉贤区中考数学一模试卷(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2009年上海市奉贤区中考数学一模试卷(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com