
【题目】(10分)如图,△ABC中,以AC为直径的⊙O与边AB交于点D,点E为⊙O上一点,连接CE并延长交AB于点F,连接ED.
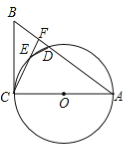
(1)若∠B+∠FED=90°,求证:BC是⊙O的切线;
(2)若FC=6,DE=3,FD=2,求⊙O的直径.
【答案】(1)详见解析;(2)⊙O的直径为9.
【解析】
试题分析: (1)由圆内接四边形对角互补可得∠A+∠DEC=180°,由邻补角的定义可得∠FED+∠DEC=180°,所以∠FED=∠A,又因∠B+∠FED=90°,即可得∠B+∠A=90°,所以∠BCA=90°,即BC是⊙O的切线;(2)由∠CFA=∠DFE,∠FED=∠A,即可得△FED∽△FAC,根据相似三角形的性质可得![]() ,带入数值即可求出AC的长.
,带入数值即可求出AC的长.
试题解析:(1)证明:∵∠A+∠DEC=180°,∠FED+∠DEC=180°,
∴∠FED=∠A,
∵∠B+∠FED=90°,
∴∠B+∠A=90°,
∴∠BCA=90°,
∴BC是⊙O的切线;
(2)解:∵∠CFA=∠DFE,∠FED=∠A,
∴△FED∽△FAC,
∴![]() ,
,
∴![]() ,
,
解得:AC=9,即⊙O的直径为9.


科目:初中数学 来源: 题型:
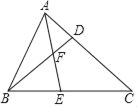
【题目】如图,已知点D、E分别在△ABC的边AC、BC上,线段BD与AE交于点F,且CDCA=CECB.
(1)求证:∠CAE=∠CBD;
(2)若![]() ,求证:ABAD=AFAE.
,求证:ABAD=AFAE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:(1)∠DCF=![]() ∠BCD;(2)EF=CF;(3)S△BEC= 2S△CEF;(4)∠DFE=3∠AEF;其中正确的结论是( )
∠BCD;(2)EF=CF;(3)S△BEC= 2S△CEF;(4)∠DFE=3∠AEF;其中正确的结论是( )
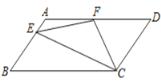
A.(1)(2)B.(1)(2)(4)C.(2)(3)(4)D.(1)(3)(4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
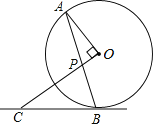
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为3,OP=1,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,有格点三角形![]() .
.

(1)写出三个顶点的坐标.
(2)将三角形![]() 沿
沿![]() 方向平移,当点
方向平移,当点![]() 的对应点
的对应点![]() 在
在![]() 轴上时,画出平移后的三角形.
轴上时,画出平移后的三角形.
(3)在给出图形中找一格点![]() (点
(点![]() 除外),使三角形
除外),使三角形![]() 与
与![]() 面积相等,并把满足条件的格点用线连起来.
面积相等,并把满足条件的格点用线连起来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某织布厂有150名工人,为了提高经济效益,增设制衣项目,已知每人每天能织布30m,或利用所织布制衣4件,制衣一件需要布1.5m,将布直接出售,每米布可获利2元,将布制成衣后出售,每件可获利25元,若每名工人每天只能做一项工作,且不计其他因素,设安排x名工人制衣.
(1)一天中制衣所获利润P是多少(用含x的式子表示);
(2)一天中剩余布所获利润Q是多少 (用含x的式子表示);.
(3)一天当中安排多少名工人制衣时,所获利润为11806元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:3+2![]() =(1+
=(1+![]() )2,善于思考的小明进行了以下探索:
)2,善于思考的小明进行了以下探索:
设a+b=(m+n![]() )2(其中a、b、m、n均为整数),则有a+b
)2(其中a、b、m、n均为整数),则有a+b![]() =m2+2n2+2mn
=m2+2n2+2mn![]() .
.
∴a=m2+2n2,b=2mn.这样小明就找到了一种把部分a+b![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b![]() =(m+n
=(m+n![]() )2,用含m、n的式子分别表示a、b,得a= ,b= ;
)2,用含m、n的式子分别表示a、b,得a= ,b= ;
(2)试着把7+4![]() 化成一个完全平方式.
化成一个完全平方式.
(3)若a是216的立方根,b是16的平方根,试计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 分别在
分别在![]() 的边
的边![]() 上运动(不与点
上运动(不与点![]() 重合),
重合),![]() 是
是![]() 的平分线,
的平分线,![]() 的延长线交角
的延长线交角![]() 的平分线于点
的平分线于点![]() .
.

(1)若![]() ,求
,求![]() 的度数.
的度数.
(2)若![]() ,求
,求![]() 的度数.
的度数.
(3)若![]() ,请用含
,请用含![]() 的代数式表示
的代数式表示![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校准备组织七年级400名学生参加北京夏令营,已知用3辆小客车和1辆大客车每次可运送学生105人;用1辆小客车和2辆大客车每次可运送学生110人;
(1)每辆小客车和每辆大客车各能坐多少名学生?
(2)若学校计划租用小客车x辆,大客车y辆,一次送完,且恰好每辆车都坐满;
①请你设计出所有的租车方案;
②若小客车每辆需租金4000元,大客车每辆需租金7600元,请选出最省钱的租车方案,并求出最少租金.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com