
分析 先求得其对称轴为x=a,再分a<0、0≤-a≤1和a>1根据二次函数的单调性分别求得其最大值,由最大值为2,可求得a的值.
解答 解:∵y=-x2+2ax+1-a,
∴其对称为x=a,开口向下,
当a<0时,在0≤x≤1上y随x的增大而减小,
∴当x=0时有最大值,最大值=1-a=2,
解得a=-1<0,符合题意;
当0≤a≤1时,y的最大值=-a2+2a2+1-a=2,
∴a=$\frac{1±\sqrt{5}}{2}$(不合题意,舍去);
当a>1时,在0≤x≤1上y随x的增大而增大,
∴最大值=-1+2a+1-a=a=2>1,
∴a=2符合题意,
综上可知a的值为-1或2.
故答案为:-1或2.
点评 本题主要考查二次函数的单调性和最值,掌握二次函数的单调性是解题的关键,注意分类讨论思想的应用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
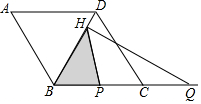 如图,菱形ABCD的边长为2,∠A=60°,点P和点Q分别从点B和点C出发,沿射线BC向右运动,且速度相同,过点Q作QH⊥BD,垂足为H,连接PH,设点P运动的距离为x(0<x≤2),△BPH的面积为S,则能反映S与x之间的函数关系的图象大致为 ( )
如图,菱形ABCD的边长为2,∠A=60°,点P和点Q分别从点B和点C出发,沿射线BC向右运动,且速度相同,过点Q作QH⊥BD,垂足为H,连接PH,设点P运动的距离为x(0<x≤2),△BPH的面积为S,则能反映S与x之间的函数关系的图象大致为 ( )| A. | 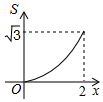 | B. | 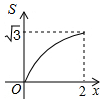 | C. | 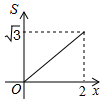 | D. | 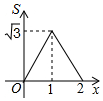 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com