
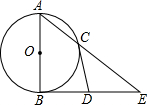 如图,AB为⊙O的直径,BE切⊙O于点C,连接AE交⊙O于点C,D是BE的中点.求证:CD是⊙O的切线.
如图,AB为⊙O的直径,BE切⊙O于点C,连接AE交⊙O于点C,D是BE的中点.求证:CD是⊙O的切线.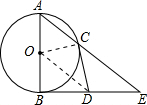 证明:连接OC、OD,
证明:连接OC、OD,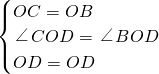 ,
,

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源:江苏省张家港市2012年中考网上阅卷适应性考试数学试题 题型:013
如图,AB为⊙O的直甲径,PD切⊙O于点C,交AB的延长线于D,且CO=CD,则∠PCA=

A.60°
B.65°
C.67.5°
D.75°
查看答案和解析>>
科目:初中数学 来源:2008年福建省福州一中高中招生(面向福州以外)综合素质测试数学试卷(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com