
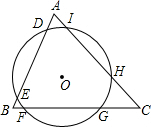
 如图,圆心O为△ABC的内心,⊙O截得的弦DE=4cm,则FG=4cm.
如图,圆心O为△ABC的内心,⊙O截得的弦DE=4cm,则FG=4cm. 分析 过O作ON⊥FG于N,OM⊥DE于M,连接OD、OF,根据垂径定理得出DE=2DM,FG=2FN,根据角平分线性质得出OM=ON,根据HL证Rt△OMD≌Rt△ONF,根据全等得出DM=FN,即可求出DE=FG.
解答 解: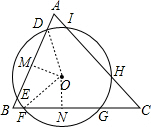
过O作ON⊥FG于N,OM⊥DE于M,连接OD、OF,
则DE=2DM,FG=2FN(垂径定理),∠OMD=∠ONF=90°,OD=OF,
∵O为△ABC的内心,
∴OM=ON,
在Rt△OMD和Rt△ONF中
$\left\{\begin{array}{l}{OD=OF}\\{OM=ON}\end{array}\right.$
∴Rt△OMD≌Rt△ONF(HL),
∴DM=FN,
∵DE=2DM,FG=2FN,
∴FG=DE,
∵DE=4cm,
∴FG=4cm,
故答案为:4.
点评 本题考查了三角形的内切圆,角平分线性质,全等三角形的性质和判定的应用,能求出DE=FG是解此题的关键,注意:角平分线上的点到这个角的两边的距离相等.


科目:初中数学 来源:2016-2017学年江苏省扬州市七年级下学期第一次月考数学试卷(解析版) 题型:单选题
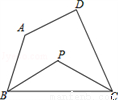
如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD的平分线交于点P,则∠P=( )
A. 90°﹣ α B. 90°+
α B. 90°+ α C.
α C.  α D. 360°﹣α
α D. 360°﹣α
查看答案和解析>>
科目:初中数学 来源:2017届山东省日照市莒县第三协作区九年级3月学业水平模拟考试数学试卷(解析版) 题型:单选题
如图,AB是⊙O的直径,BC⊥AB,垂足为点B,连接CO并延长交⊙O于点D、E,连接AD并延长交BC于点F.则下列结论正确的有( )
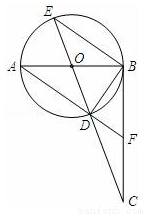
①∠CBD=∠CEB;②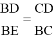 ;③点F是BC的中点;④若
;③点F是BC的中点;④若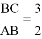 ,则tanE=
,则tanE=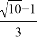 .
.
A. ①② B. ③④ C. ①②④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且AB=15cm,BC=20cm,CA=25cm.
如图,△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且AB=15cm,BC=20cm,CA=25cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $±\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com