
 如图,已知过点(
如图,已知过点( ,-
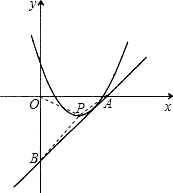
,- )的直线y=kx+b与x轴、y轴的交点分别为A、B,且经过第一、三、四象限,它与抛物线y=x2-4x+3只有一个公共点.
)的直线y=kx+b与x轴、y轴的交点分别为A、B,且经过第一、三、四象限,它与抛物线y=x2-4x+3只有一个公共点. ,-
,- ),
), =
= k+b,
k+b, -
- k;
k; k-
k- ,
,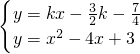 消去y,得:
消去y,得: k+
k+ )=0,
)=0, k+
k+ )=0,
)=0, ;
;
 ;
; ;
; ,0),B(0,-
,0),B(0,- ),
), =
=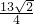 ;
; OA•1+
OA•1+ OB•2+
OB•2+ AB•d=
AB•d= OA•OB,
OA•OB,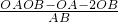 =
=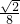 ,
,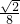 .
. ,一
,一 )在直线y=kx+b上,则此点坐标满足该一次函数解析式,将其代入即可求出k、b的关系式;用k代替b后,联立抛物线的解析式,可得关于x的一元二次方程,由于两个函数只有一个公共点,那么方程的根的判别式△=0,可据此求出k的值.
)在直线y=kx+b上,则此点坐标满足该一次函数解析式,将其代入即可求出k、b的关系式;用k代替b后,联立抛物线的解析式,可得关于x的一元二次方程,由于两个函数只有一个公共点,那么方程的根的判别式△=0,可据此求出k的值.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
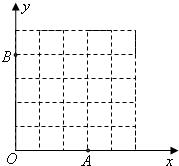 24、我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
24、我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.查看答案和解析>>
科目:初中数学 来源: 题型:
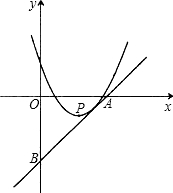 如图,已知过点(
如图,已知过点(| 3 |
| 2 |
| 7 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2007-2008学年江苏省苏州市吴中区九年级(上)期末数学试卷(解析版) 题型:解答题
 ,-
,- )的直线y=kx+b与x轴、y轴的交点分别为A、B,且经过第一、三、四象限,它与抛物线y=x2-4x+3只有一个公共点.
)的直线y=kx+b与x轴、y轴的交点分别为A、B,且经过第一、三、四象限,它与抛物线y=x2-4x+3只有一个公共点.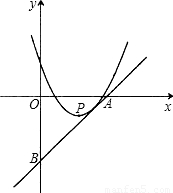
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com