
分析 由x2-2x-1=0得到x2-2x=1.然后将所求的代数式进行变形为:x2(x2-2x)+x(x2-2x)-3(x2-2x)-13x+5,然后将其整体代入进行求值.
解答 解:解方程x2-2x-1=0,得
x=1±$\sqrt{2}$.
∵x2-2x-1=0,
∴x2-2x=1,
∴x4-x3-5x2-7x+5,
=x2(x2-2x)+x(x2-2x)-3(x2-2x)-13x+5,
=x2+x-3-13x+5,
=3-10x.
则原式=3-10(1+±$\sqrt{2}$)=-7±10$\sqrt{2}$.
点评 本题考查了因式分解的应用:利用因式分解解决求值问题;利用因式分解解决证明问题;利用因式分解简化计算问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
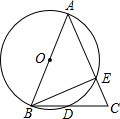 如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,给出以下五个结论:①∠EBC=22.5°;②BD=DC;③AE=2EC;④劣弧$\widehat{AE}$是劣弧$\widehat{BD}$的2倍;⑤AE=BC,其中正确的序号是①②④.
如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,给出以下五个结论:①∠EBC=22.5°;②BD=DC;③AE=2EC;④劣弧$\widehat{AE}$是劣弧$\widehat{BD}$的2倍;⑤AE=BC,其中正确的序号是①②④.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com