

分析 (1)由旋转的性质可知:AF=AG,∠DAF=∠BAG,接下来在证明∠GAE=∠FAE,然后依据SAS证明△GAE≌△FAE即可;
(2)将△ABM逆时针旋转90°得△ADM′.在△NM′D中依据勾股定理可证明NM′2=ND2+DM′2,接下来证明△AMN≌△ANM′,于的得到MN=NM′,最后再由BM=DM′证明即可.
解答 解:(1)由旋转的性质可知:AF=AG,∠DAF=∠BAG.
∵四边形ABCD为正方形,
∴∠BAD=90°.
又∵∠EAF=45°,
∴∠BAE+∠DAF=45°.
∴∠BAG+∠BAE=45°.
∴∠GAE=∠FAE.
在△GAE和△FAE中$\left\{\begin{array}{l}{AG=AF}\\{∠GAE=∠FAE}\\{AE=AE}\end{array}\right.$,
∴△GAE≌△FAE(SAS);
(2)如图所示:将△ABM逆时针旋转90°得△ADM′.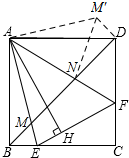
∵四边形ABCD为正方形,
∴∠ABD=∠ADB=45°.
由旋转的性质可知:∠ABM=∠ADM′=45°,BE=DM′.
∴∠NDM′=90°.
∴NM′2=ND2+DM′2.
∵∠EAM′=90°,∠EAF=45°,
∴∠EAF=∠FAM′=45°.
在△AMN和△ANM′中,$\left\{\begin{array}{l}{AM=AM′}\\{∠MAN=M′AN}\\{AN=AN}\end{array}\right.$,
∴△AMN≌△ANM′(SAS).
∴MN=NM′.
又∵BM=DM′,
∴MN2=ND2+BM2.
点评 本题主要考查的是四边形的综合应用,解答本题主要应用了旋转的性质、全等三角形的性质和判定、勾股定理的应用,正方形的性质,依据旋转的性质构造全等三角形和直角三角形是解题的关键.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:解答题
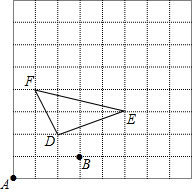 如图,用(0,0)表示A点的位置,用(3,1)表示B点的位置,那么:
如图,用(0,0)表示A点的位置,用(3,1)表示B点的位置,那么:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
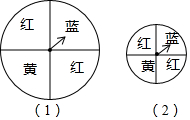 如图,两个用来摇奖的转盘,其中说法正确的是( )
如图,两个用来摇奖的转盘,其中说法正确的是( )| A. | 转盘(1)中蓝色区域的面积比转盘(2)中的蓝色区域面积要大,所以摇转盘(1)比摇转盘(2)时,蓝色区域得奖的可能性大 | |
| B. | 两个转盘中指针指向蓝色区域的机会一样大 | |
| C. | 转盘(1)中,指针指向红色区域的概率是$\frac{1}{3}$ | |
| D. | 在转盘(2)中只有红、黄、蓝三种颜色,指针指向每种颜色的概率都是$\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
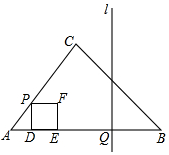 如图,在△ABC中,AB=7,BC=4$\sqrt{2}$,∠B=45°,动点P、Q同时出发,点P沿A-C-B运动,在边AC的速度为每秒1个单位长度,在边CB的速度为每秒$\sqrt{2}$个单位长度;点Q沿B-A-B以每秒2个单位长度的速度运动,其中一个动点到达终点时,另一个动点也停止运动,在运动过程中,过点P作AB的垂线与AB交于点D,以PD为边向由作正方形PDEF;过点Q作AB的垂线l.设正方形PDEF与△ABC重叠部分图形的面积为y(平方单位),运动时间为t(s).
如图,在△ABC中,AB=7,BC=4$\sqrt{2}$,∠B=45°,动点P、Q同时出发,点P沿A-C-B运动,在边AC的速度为每秒1个单位长度,在边CB的速度为每秒$\sqrt{2}$个单位长度;点Q沿B-A-B以每秒2个单位长度的速度运动,其中一个动点到达终点时,另一个动点也停止运动,在运动过程中,过点P作AB的垂线与AB交于点D,以PD为边向由作正方形PDEF;过点Q作AB的垂线l.设正方形PDEF与△ABC重叠部分图形的面积为y(平方单位),运动时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明的手机没电了,现有一个只含A,B,C,D四个同型号插座的插线板(如图,假设每个插座都适合所有的充电插头,且被选中的可能性相同),请计算:
小明的手机没电了,现有一个只含A,B,C,D四个同型号插座的插线板(如图,假设每个插座都适合所有的充电插头,且被选中的可能性相同),请计算:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 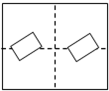 | B. | 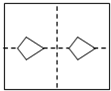 | C. | 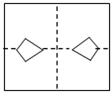 | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com