
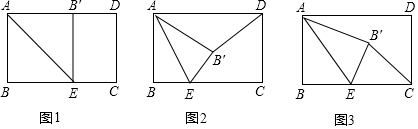
分析 (1)由折叠性质知∠AB′E=∠B=90°,∠1=∠2=$\frac{1}{2}$∠BAD=45°,即可得;
(2)作B′F⊥AD,由△AEB≌△AEB′且∠BAE=30°知∠BAE=∠B′AE=∠B′AF=30°、AB=AB′=2,可得B′F=1,即可得答案;
(3)由折叠性质得出AB=AB′=2、∠B=∠AB′E=90°、BE=EC=$\frac{1}{2}$BC=$\frac{3}{2}$,设B′P=x,AP=y,证△APB′∽△B′QE$\frac{AP}{B′Q}$=$\frac{B′P}{EQ}$=$\frac{AB′}{B′E}$即$\frac{y}{2-x}$=$\frac{x}{y-\frac{3}{2}}$=$\frac{2}{\frac{3}{2}}$,求得x、y的值,从而得出B′F=$\frac{36}{25}$、CF=$\frac{27}{25}$,利用勾股定理得出答案.
解答 解:(1)如图1,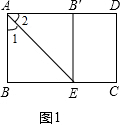
由题意知△AEB≌△AEB′,
∴∠AB′E=∠B=90°,∠1=∠2=$\frac{1}{2}$∠BAD=45°,
∴△AEB′为等腰直角三角形;
(2)如图2,作B′F⊥AD于点F,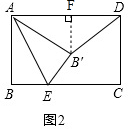
∵△AEB≌△AEB′,且∠BAE=30°,
∴∠BAE=∠B′AE=∠B′AF=30°,AB=AB′=2,
在Rt△AB′F中,B′F=$\frac{1}{2}$AB′=1,
∴S△ADB′=$\frac{1}{2}$•AD•B′F=$\frac{1}{2}$×3×1=$\frac{3}{2}$;
(3)如图3,过点B′作B′P⊥AD于点P,延长PB′交BC于点Q,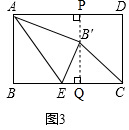
∵△AEB≌△AEB′,
∴AB=AB′=2,∠B=∠AB′E=90°,
∵E为BC中点,且BC=AD=3,
∴BE=EC=$\frac{1}{2}$BC=$\frac{3}{2}$,
∵AD∥BC,B′P⊥AD,
∴PQ⊥BC,
∴∠APB′=∠B′QE=90°,
∴∠PAB′+∠PB′A=90°,
又∵∠AB′E=90°,
∴∠PB′A+∠EB′Q=90°,
∴∠PAB′=∠QB′E,
∴△APB′∽△B′QE,
设B′P=x,AP=y,
则B′Q=2-x,EQ=BQ-BE=AP-BE=y-$\frac{3}{2}$,
由$\frac{AP}{B′Q}$=$\frac{B′P}{EQ}$=$\frac{AB′}{B′E}$可得$\frac{y}{2-x}$=$\frac{x}{y-\frac{3}{2}}$=$\frac{2}{\frac{3}{2}}$,
解得:x=$\frac{14}{25}$、y=$\frac{48}{25}$,
即B′P=$\frac{14}{25}$、AP=$\frac{48}{25}$,
则B′F=2-$\frac{14}{25}$=$\frac{36}{25}$,CF=BC-BF=3-$\frac{48}{25}$=$\frac{27}{25}$,
∴B′C=$\sqrt{B′{F}^{2}+C{F}^{2}}$=$\sqrt{(\frac{36}{25})^{2}+(\frac{27}{25})^{2}}$=$\frac{9}{5}$.
点评 本题主要考查四边形的综合问题,熟练掌握矩形的判定与性质、折叠的性质、相似三角形的判定与性质及勾股定理是解题的关键.


科目:初中数学 来源: 题型:解答题
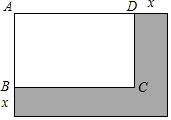 如图,矩形ABCD的长AD=5cm,宽AB=3cm,长和宽都增加xcm,那么面积增加ycm2.
如图,矩形ABCD的长AD=5cm,宽AB=3cm,长和宽都增加xcm,那么面积增加ycm2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,⊙C过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,6),⊙C的半径长为5,则C点坐标为( )
如图,⊙C过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,6),⊙C的半径长为5,则C点坐标为( )| A. | (3,4) | B. | (4,3) | C. | (-4,3) | D. | (-3,4) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
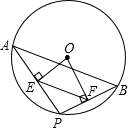 如图,点A、B是⊙O上两点,AB=10,点P是⊙O上的动点(P与A、B不重合),连结AP、PB,过点O分别作OE⊥AP于点E,OF⊥AP于点E,OF⊥PB于点F,则EF=( )
如图,点A、B是⊙O上两点,AB=10,点P是⊙O上的动点(P与A、B不重合),连结AP、PB,过点O分别作OE⊥AP于点E,OF⊥AP于点E,OF⊥PB于点F,则EF=( )| A. | 4 | B. | 5 | C. | 5.5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,已知矩形OABC的顶点A在x轴上,OA=4,OC=3.点D为BC边上一点,以AD为一边在与点B的同侧作正方形ADEF,连接OE,当点D在边BC上运动时,OE的长度的最小值是多少?
如图,在平面直角坐标系中,已知矩形OABC的顶点A在x轴上,OA=4,OC=3.点D为BC边上一点,以AD为一边在与点B的同侧作正方形ADEF,连接OE,当点D在边BC上运动时,OE的长度的最小值是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com