
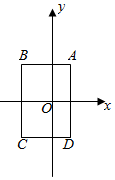
 如图所示,在平面直角坐标系中,已知点A (1,2),B (-2,2),C (-2,-2),D(1,-2),把一根长为2017个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A→D→C→B→A…的顺序紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是( )
如图所示,在平面直角坐标系中,已知点A (1,2),B (-2,2),C (-2,-2),D(1,-2),把一根长为2017个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A→D→C→B→A…的顺序紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是( )| A. | (1,2) | B. | (0,2) | C. | (1,1) | D. | (1,-2) |
分析 根据点A、B、C、D的坐标可得出AB、BC的长度以及四边形ABCD为矩形,进而可求出矩形ABCD的周长,根据细线的缠绕方向以及细线的长度即可得出细线的另一端所在位置,此题得解.
解答 解:∵A(1,2),B(-2,2),C(-2,-2),D(1,-2),
∴AB=CD=3,AD=BC=4,且四边形ABCD为矩形,
∴矩形ABCD的周长C矩形ABCD=2(AB+BC)=14.
∵2017=144×14+1,
∴细线的另一端落在AD上,坐标为(1,1).
故选C.
点评 本题考查了规律型中点的坐标、矩形的判定以及矩形的周长,根据矩形的周长结合细线的长度找出细线终点所在的位置是解题的关键.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:填空题
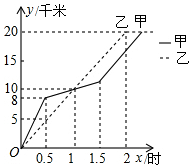 在20km越野赛中,甲乙两选手的行程y(单位:km)随时间x(单位:h)变化的图象如图所示,根据图中提供的信息,有下列说法:
在20km越野赛中,甲乙两选手的行程y(单位:km)随时间x(单位:h)变化的图象如图所示,根据图中提供的信息,有下列说法:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. | 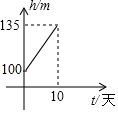 | C. | 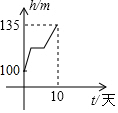 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 900元 | B. | 920元 | C. | 960元 | D. | 980元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
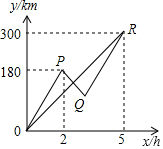 已知A,B两地公路长300km,甲、乙两车同时从A地出发沿同一公路驶往B地,2小时后,甲车接到电话需返回这条公路上的C处取回货物,于是甲车立即原路返回C,取了货物又立即赶往B地(取货物的时间忽略不计),结果两车同时到达B地.两车的速度始终保持不变,设两车出发x小时后,甲、乙距离A地的距离分别为y1(km)和y2(km),它们的函数图象分别是折线OPQR和线段OR.
已知A,B两地公路长300km,甲、乙两车同时从A地出发沿同一公路驶往B地,2小时后,甲车接到电话需返回这条公路上的C处取回货物,于是甲车立即原路返回C,取了货物又立即赶往B地(取货物的时间忽略不计),结果两车同时到达B地.两车的速度始终保持不变,设两车出发x小时后,甲、乙距离A地的距离分别为y1(km)和y2(km),它们的函数图象分别是折线OPQR和线段OR.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com