
 如图,有一个圆锥形粮堆,正三角形ABC的边长为6m,粮堆母线AC的中点P处有一只鼠正在吃粮食,此时小猫正在B处,它要沿圆锥侧面P处捉老鼠,小猫所经过的最短路程是
如图,有一个圆锥形粮堆,正三角形ABC的边长为6m,粮堆母线AC的中点P处有一只鼠正在吃粮食,此时小猫正在B处,它要沿圆锥侧面P处捉老鼠,小猫所经过的最短路程是 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
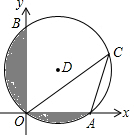 如图,在平面直角坐标系中,已知⊙D经过原点O,与x轴、y轴分别交于A、B两点,点B坐标为(0,2
如图,在平面直角坐标系中,已知⊙D经过原点O,与x轴、y轴分别交于A、B两点,点B坐标为(0,2| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
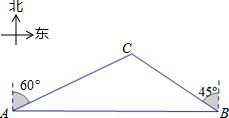 如图,一天,我国一渔政船航行到A处时,发现正东方向的我领海区域B处有一可疑渔船,可疑渔船正向西北方向航行,我渔政船立即沿北偏东60°方向航行,在我领海区域的C处截获可疑渔船.我渔政船的航行路程AC为18是海里,问可疑渔船的航行路程BC是多少海里?(结果保留根号)
如图,一天,我国一渔政船航行到A处时,发现正东方向的我领海区域B处有一可疑渔船,可疑渔船正向西北方向航行,我渔政船立即沿北偏东60°方向航行,在我领海区域的C处截获可疑渔船.我渔政船的航行路程AC为18是海里,问可疑渔船的航行路程BC是多少海里?(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:
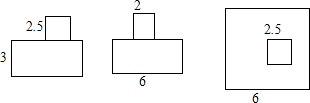 已知一个模型的三视图如图所示,(单位:m)
已知一个模型的三视图如图所示,(单位:m)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com