
| 售价x(元/件) | … | 30 | 40 | 50 | 60 | … |
| 日销售量y(件) | … | 500 | 400 | 300 | 200 | … |
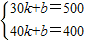 ,
,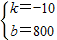 ,
,

 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
|
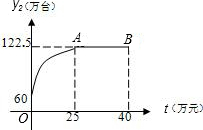 其中点A为抛物线的顶点.
其中点A为抛物线的顶点.查看答案和解析>>
科目:初中数学 来源: 题型:
| 售价x(元/件) | … | 30 | 40 | 50 | 60 | … |
| 日销售量y(件) | … | 500 | 400 | 300 | 200 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
 某公司开发了一种新型的家电产品,又适逢“家电下乡”的优惠政策.现投资50万元用于该产品的广告促销,已知该产品的本地销售量y1(万台)与本地的广告费用x(万元)之间的函数关系满足y1=3x(0≤x≤50); 该产品的外地销售量y2(万台)与外地广告费用t(万元)之间的函数关系可用如图所示的抛物线和线段AB来表示.其中点A为抛物线的顶点.
某公司开发了一种新型的家电产品,又适逢“家电下乡”的优惠政策.现投资50万元用于该产品的广告促销,已知该产品的本地销售量y1(万台)与本地的广告费用x(万元)之间的函数关系满足y1=3x(0≤x≤50); 该产品的外地销售量y2(万台)与外地广告费用t(万元)之间的函数关系可用如图所示的抛物线和线段AB来表示.其中点A为抛物线的顶点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 售价x(元/件) | … | 30 | 40 | 50 | 60 | … |
| 日销售量y(件) | … | 500 | 400 | 300 | 200 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com