练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，将一个长、宽分别为8、4的长方形纸片ABCD折叠，使C点与A点重合，则折痕EF的长是多少？

    解：设BE，连AE，则AE=CE，有，，

      

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    图①是一张长与宽不相等的矩形纸片，同学们都知道按图②所示的折叠方法可以裁剪出一个正方形纸片和一个矩形纸片（如图③），
    精英家教网
    （1）实验：
    将这两张纸片分别按图④、⑤所示的折叠方法进行：
    精英家教网
    请你分别在图④、⑤的最右边的图形中用虚线画出折痕，并顺次连接每条折痕的端点，所围成的四边形分别是什么四边形？
    （2）当原矩形纸片的AB=4，BC=6时，分别求出（1）中连接折痕各端点所得四边形的面积，并求出它们的面积比；
    （3）当纸片ABCD的长和宽满足怎样的数量关系时先后得到的两个四边形的面积比等于（2）所得到的两个四边形的面积比？
    （4）用（2）中所得到的两张纸片，分别裁剪出那两个四边形，用剩下的8张纸片拼出两个周长不相等的等腰梯形，用图表示并标明主要数据，分别求出两梯形的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图所示，边长为a的大正方形中有一个边长为b的小正方形．

    （1）请用字母a和b表示出图中阴影部分的面积；
    （2）将阴影部分还能拼成一个长方形，如图乙这个长方形的长和宽分别是多少？表示出阴影部分的面积；
    （3）比较（1）和（2）的结果，可以验证平方差公式吗？请给予解答．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    小明将一个底为正方形，高为m的无盖盒子展开，如图①所示，测得其边长为n，
    （1）请你计算无盖纸盒的表面展开图的面积S1（即图中阴影部分的面积）．
    （2）将阴影部分拼成一个长方形如图②所示，这个长方形的长和宽分别是多少？面积S2是多少？
    （3）比较（1）、（2）的结果，你得出什么结论？

    查看答案和解析>>

    科目：初中数学 来源：探秘数学　　九年级上 题型：044

    如图，将一块长30cm、宽20cm的矩形铁片四角都截去一个边长相等的小正方形，再把四边折起来做成一只无盖的盒子，使底面积是原来铁片面积的三分之一，求盒子的容积．

    查看答案和解析>>

    科目：初中数学 来源：2014届江苏省江阴华士片七年级下学期期中考试数学卷（解析版） 题型：解答题

    如图：用两个边长为a、b、c的直角三角形和一个边长为c的等腰直角三角形拼成一个直角梯形，试用不同的方法计算这个图形的面积。（本题6分）

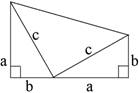
     （1）你能得到关于a，b，c的一个等式吗？写出你的过程。

      （2）请用一句话描述你的发现：在直角三角形中，                              

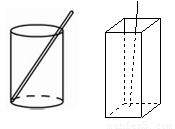
      （3）请应用你学到的新知识解决下面这个问题：将一根长为30cm的筷子置于底面直径为5cm，高12cm的圆柱形的空水杯中，则露出杯子外面的长度最短是____cm ,最长是____ cm.如果把圆柱体换成一个长，宽，高分别为6,8,24的无盖长方体盒子。那么这根筷子露出盒子外面的长度最短是____cm

     

    查看答案和解析>>

    同步练习册答案