

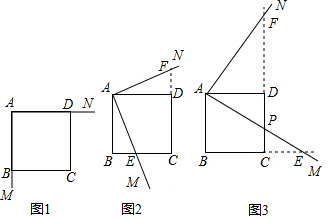
���� ��1������A��B��������������ߵĽ���ʽ���õ�����a��b�ķ��̣��Ӷ������a��b��ֵ��
��2�����P������ΪP��m��m2-6m+4������ƽ���ı��ε����Ϊ30��֪S��CBP=15����S��CBP=S����CEDP-S��CEB-S��PBD���õ�����m�ķ������m��ֵ���Ӷ�����õ�P�����ꣻ
��3������֤����EAB�ס�NMB���Ӷ��ɵõ�NB=$\frac{3}{2}$����MBΪԲ��ֱ��ʱ��NB�����ֵ��
��� �⣺��1������A��B��������������ߵĽ���ʽ�ã�$\left\{\begin{array}{l}{a+b+4=-1}\\{25a+5b+4=-1}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{a=1}\\{b=-6}\end{array}\right.$��
�������ߵý���ʽΪy=x2-6x+4��
��2����ͼ��ʾ��
���P������ΪP��m��m2-6m+4��
��ƽ���ı��ε����Ϊ30��
��S��CBP=15������S��CBP=S����CEDP-S��CEB-S��PBD��
��$\frac{1}{2}$m��5+m2-6m+4+1��-$\frac{1}{2}$��5��5-$\frac{1}{2}$��m-5����m2-6m+5��=15��
����ã�m2-5m-6=0��
��ã�m=6����m=-1��
���P��������6��4����-1��11����
��3������AB��EB��
��AE��Բ��ֱ����
���ABE=90�㣮
���ABE=��MBN��
�֡ߡ�EAB=��EMB��
���EAB�ס�NMB��
��A��1��-1����B��5��-1����
���O1�ĺ�����Ϊ3��
��x=0���������ߵĽ���ʽ�ã�y=4��
���C��������0��4����
���O1��������3��m����
��O1C=O1A��
��$\sqrt{{3}^{2}+��m-4��^{2}}$=$\sqrt{{2}^{2}+��m+1��^{2}}$��
��ã�m=2��
���O1��������3��2����
��O1A=$\sqrt{{3}^{2}+��2-4��^{2}}$=$\sqrt{13}$��
��Rt��ABE�У��ɹ��ɶ����ã�BE=$\sqrt{A{E}^{2}-A{B}^{2}}$=$\sqrt{2��\sqrt{13}��^{2}-{4}^{2}}$=6��
���E��������5��5����
��AB=4��BE=6��
�ߡ�EAB�ס�NMB��
��$\frac{AB}{EB}$=$\frac{MB}{NB}$��
��$\frac{4}{6}$=$\frac{MB}{NB}$��
��NB=$\frac{3}{2}$MB��
�൱MBΪֱ��ʱ��MB���ʱNB���
��MB=AE=2$\sqrt{13}$��
��NB=$\frac{3}{2}$��2$\sqrt{13}$=3$\sqrt{13}$��
���� ������Ҫ������Ƕ��κ������ۺ�Ӧ�ã��⣨1���Ĺؼ��Ǵ���ϵ�������⣨2���Ĺؼ�����������ĺͲ�ó�����m�ķ��̣��⣨3���Ĺؼ��������������������ε��ж������ʵó�$\frac{AB}{EB}$=$\frac{MB}{NB}$����������Բ�����ʣ�ֱ�����


 ѧ���쳵�����ּ��ں�����ҵϵ�д�
ѧ���쳵�����ּ��ں�����ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��Ϊ�˲��������ڸ��ٹ�·ˮƽ�����ϵĽ�ͨ��ʾ�Ƶĸ߶�CD���ھ�M���4��A������þ�ʾ���¶�D������Ϊ45�㣬�ٱ�ֱ��ǰ��8����B������B����þ�ʾ���϶�C������Ϊ30�㣬��ʾ�Ƶĸ߶�CD���������ȷ��0.1�ף��ο����ݣ�$\sqrt{2}$��1.41��$\sqrt{3}$��1.73��
��ͼ��Ϊ�˲��������ڸ��ٹ�·ˮƽ�����ϵĽ�ͨ��ʾ�Ƶĸ߶�CD���ھ�M���4��A������þ�ʾ���¶�D������Ϊ45�㣬�ٱ�ֱ��ǰ��8����B������B����þ�ʾ���϶�C������Ϊ30�㣬��ʾ�Ƶĸ߶�CD���������ȷ��0.1�ף��ο����ݣ�$\sqrt{2}$��1.41��$\sqrt{3}$��1.73���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
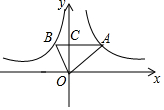 ��ͼ����ƽ��ֱ������ϵ�У���A�ں���y=$\frac{3}{x}$ ��x��0����ͼ���ϣ���B�ں���y=$\frac{k}{x}$ ��x��0����ͼ���ϣ�AB��y���ڵ�C����AC=3BC����k��ֵΪ��������
��ͼ����ƽ��ֱ������ϵ�У���A�ں���y=$\frac{3}{x}$ ��x��0����ͼ���ϣ���B�ں���y=$\frac{k}{x}$ ��x��0����ͼ���ϣ�AB��y���ڵ�C����AC=3BC����k��ֵΪ��������| A�� | -1 | B�� | 1 | C�� | -2 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
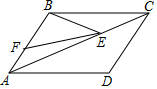 ��֪����ͼ����?ABCD�У�BE��CE�ֱ�ƽ�֡�ABC����BCD��EΪAD�ϣ�BE=12cm��CE=5cm����?ABCD���ܳ�Ϊ39cm��
��֪����ͼ����?ABCD�У�BE��CE�ֱ�ƽ�֡�ABC����BCD��EΪAD�ϣ�BE=12cm��CE=5cm����?ABCD���ܳ�Ϊ39cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
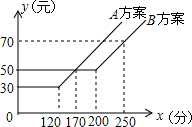 ��ͼ��ij���Ź�˾�ṩ��A��B���ַ������ƶ�ͨѶ����y��Ԫ����ͨ��ʱ��x��Ԫ��֮��Ĺ�ϵ�����н��ۣ�
��ͼ��ij���Ź�˾�ṩ��A��B���ַ������ƶ�ͨѶ����y��Ԫ����ͨ��ʱ��x��Ԫ��֮��Ĺ�ϵ�����н��ۣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com