1
分析:设B点坐标为(a,a),A点坐标为(m,a),则C点坐标为(a,0),D点坐标为(a,

a),作DE∥OC,根据平行线性质得∠AED=∠AOC,而∠AOC=∠OAD,则∠AED=∠EAD,得到DA=DE,由DE为梯形ABCO的中位线,DE=

(AB+OC)=

(a-m+a)=a-

m,在Rt△ABD中利用勾股定理得到(a-m)
2+

a
2=(a-

m)
2,可解得a
1=3m,a
2=m(舍去),然后利用S
△AOD=S
梯形ABCO-S
△ABD-S
△ODC=

建立关于m的方程,解方程得到满足条件的m的值,确定A点坐标,再把A点坐标代入反比例解析式可求出k的值.
解答:设B点坐标为(a,a),A点坐标为(m,a),则C点坐标为(a,0),D点坐标为(a,

a),
作DE∥OC,如图,
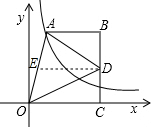
则∠AED=∠AOC,
∵∠AOC=∠OAD,
∴∠AED=∠EAD,
∴DA=DE,
∵D点为BC的中点,
∴DE为梯形ABCO的中位线,
∴DE=

(AB+OC)=

(a-m+a)=a-

m,
∴DA=a-

m,
在Rt△ABD中,AB
2+BD
2=AD
2,即(a-m)
2+

a
2=(a-

m)
2,
整理得a
2-4ma+3m
2=0,解得a
1=3m,a
2=m(舍去),
∵S
△AOD=S
梯形ABCO-S
△ABD-S
△ODC,
∴

(2m+3m)•3m-

•2m•

m-

•3m•

m=

,
解得m
1=

,m
2=-

(舍去),
∴A点坐标为(

,

),
把A(

,

)代入y=

中得k=

×

=1.
故答案为:1.
点评:本题考查了反比例函数的综合题:反比例函数y=

图象上的点满足其解析式;当k>0,反比例函数图象分布在第一、三象限,在每一象限y随x的增大而减小;利用梯形中位线的性质可得到线段之间的相等关系,运用勾股定理可进行几何计算.

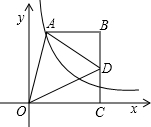 如图,点A在双曲线y=
如图,点A在双曲线y= 上,点C在x轴正半轴上,过点A,C分别作x轴,y轴的平行线,交点为B,D为BC的中点,连接AD,OD.若OC=BC,∠OAD=∠AOC,S△AOD=
上,点C在x轴正半轴上,过点A,C分别作x轴,y轴的平行线,交点为B,D为BC的中点,连接AD,OD.若OC=BC,∠OAD=∠AOC,S△AOD= ,则k的值为________.
,则k的值为________. a),作DE∥OC,根据平行线性质得∠AED=∠AOC,而∠AOC=∠OAD,则∠AED=∠EAD,得到DA=DE,由DE为梯形ABCO的中位线,DE=
a),作DE∥OC,根据平行线性质得∠AED=∠AOC,而∠AOC=∠OAD,则∠AED=∠EAD,得到DA=DE,由DE为梯形ABCO的中位线,DE= (AB+OC)=
(AB+OC)= (a-m+a)=a-
(a-m+a)=a- m,在Rt△ABD中利用勾股定理得到(a-m)2+
m,在Rt△ABD中利用勾股定理得到(a-m)2+ a2=(a-
a2=(a- m)2,可解得a1=3m,a2=m(舍去),然后利用S△AOD=S梯形ABCO-S△ABD-S△ODC=
m)2,可解得a1=3m,a2=m(舍去),然后利用S△AOD=S梯形ABCO-S△ABD-S△ODC= 建立关于m的方程,解方程得到满足条件的m的值,确定A点坐标,再把A点坐标代入反比例解析式可求出k的值.
建立关于m的方程,解方程得到满足条件的m的值,确定A点坐标,再把A点坐标代入反比例解析式可求出k的值. a),
a), 则∠AED=∠AOC,
则∠AED=∠AOC, (AB+OC)=
(AB+OC)= (a-m+a)=a-
(a-m+a)=a- m,
m, m,
m, a2=(a-
a2=(a- m)2,
m)2, (2m+3m)•3m-
(2m+3m)•3m- •2m•
•2m• m-
m- •3m•
•3m• m=
m= ,
, ,m2=-
,m2=- (舍去),
(舍去), ,
, ),
), ,
, )代入y=
)代入y= 中得k=
中得k= ×
× =1.
=1. 图象上的点满足其解析式;当k>0,反比例函数图象分布在第一、三象限,在每一象限y随x的增大而减小;利用梯形中位线的性质可得到线段之间的相等关系,运用勾股定理可进行几何计算.
图象上的点满足其解析式;当k>0,反比例函数图象分布在第一、三象限,在每一象限y随x的增大而减小;利用梯形中位线的性质可得到线段之间的相等关系,运用勾股定理可进行几何计算. 

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案 如图,点A在双曲线y=
如图,点A在双曲线y= (2012•三明)如图,点A在双曲线y=
(2012•三明)如图,点A在双曲线y=