
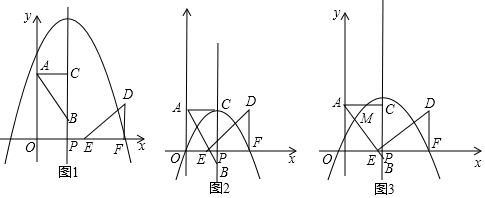
分析 (1)分两种情形讨论求出OF即可解决问题;
(2)①由题意抛物线的顶点坐标(3,3),经过(0,0),F(6,0),利用待定系数法即可解决问题;
②(ⅰ)设平移后的抛物线为y=-$\frac{1}{3}$(x-3)2+m,把F(3+t,0)代入得到m=$\frac{1}{3}$t2,推出抛物线的解析式为y=-$\frac{1}{3}$(x-3)2+$\frac{1}{3}$t2,当抛物线经过点A(0,t)时,t=-3+$\frac{1}{3}$t2,解得t=$\frac{3±\sqrt{5}}{2}$,由此即可解决问题;
(ⅱ)易知直线AB的解析式为y=-$\frac{3}{4}$x+t,由$\left\{\begin{array}{l}{y=-\frac{3}{4}x+t}\\{y=-\frac{1}{3}(x-3)^{2}+\frac{1}{3}{t}^{2}}\end{array}\right.$,把M(x0,y0)代入,消去y0得到t2-3t-x02+10x0-9=0,由题意△=0,求出x0即可解决问题.
解答 解:(1)∵Rt△ABC中,斜边AB=5,直角边AC=3,
∴BC=4,
∵PC=PF=OA,OP=AC=3,
当t≥0时,OF=OP+PF=3+t,
当t<0时.OF=OP-PF=3-(-t)=3+t,
∴F(3+t,0).
(2)①由题意抛物线的顶点坐标(3,3),经过(0,0),F(6,0),
∴设抛物线的解析式为y=a(x-3)2+3,(0,0)代入得到a=-$\frac{1}{3}$,
∴抛物线的解析式为y=-$\frac{1}{3}$(x-3)2+3.
②(ⅰ)设平移后的抛物线为y=-$\frac{1}{3}$(x-3)2+m,把F(3+t,0)代入得到m=$\frac{1}{3}$t2,
∴抛物线的解析式为y=-$\frac{1}{3}$(x-3)2+$\frac{1}{3}$t2,
当抛物线经过点A(0,t)时,t=-3+$\frac{1}{3}$t2,解得t=$\frac{3±\sqrt{5}}{2}$,
由题意,当抛物线与线段AB始终有交点M(x0,y0)时,t的取值范围$\frac{3-\sqrt{5}}{2}$≤t≤$\frac{3+\sqrt{5}}{2}$.
(ⅱ)易知直线AB的解析式为y=-$\frac{3}{4}$x+t,
由$\left\{\begin{array}{l}{y=-\frac{3}{4}x+t}\\{y=-\frac{1}{3}(x-3)^{2}+\frac{1}{3}{t}^{2}}\end{array}\right.$,把M(x0,y0)代入,消去y0得到t2-3t-x02+10x0-9=0,
由题意△=0,
∴9+4x02-40x0+36=0,
解得x0=$\frac{10±\sqrt{55}}{2}$,
∴t=$\frac{3}{2}$,
∴M($\frac{10+\sqrt{55}}{2}$,$\frac{-18-3\sqrt{55}}{8}$)或($\frac{10-\sqrt{55}}{2}$,$\frac{-18+3\sqrt{55}}{8}$).
点评 本题考查二次函数综合题、一次函数的性质、待定系数法、一元二次方程的根的判别式等知识,解题的关键是理解题意,灵活运用待定系数法解决问题,学会把问题作为一元二次方程解决,体现了数形结合的思想,属于中考压轴题.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{a}^{2}+{b}^{2}}$ | B. | $\sqrt{\frac{a}{b}}$ | C. | $\sqrt{25a}$ | D. | $\sqrt{4a+4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
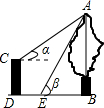 学习完解直角三角形知识,同学们利用它求我校某平房前一棵大树的高度,如图,大树AB与平房CD底部在同一平地,知道二层平房CD高为6米,在平房顶部点C测得树顶A点的仰角α=30°,从平房底部向树的方向水平前进2米到达点E,在点E处测得大树顶A的仰角β=60°,请你帮同学们求出这棵大树高度AB(结果保留根号)
学习完解直角三角形知识,同学们利用它求我校某平房前一棵大树的高度,如图,大树AB与平房CD底部在同一平地,知道二层平房CD高为6米,在平房顶部点C测得树顶A点的仰角α=30°,从平房底部向树的方向水平前进2米到达点E,在点E处测得大树顶A的仰角β=60°,请你帮同学们求出这棵大树高度AB(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
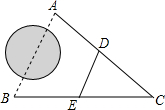 如图,A,B两地无法直接测量距离,现在地面上选一点C,连接CA,CB,分别取CA,CB的中点D,E,若测得DE的长为30m,那么A,B两地间的距离是60m.
如图,A,B两地无法直接测量距离,现在地面上选一点C,连接CA,CB,分别取CA,CB的中点D,E,若测得DE的长为30m,那么A,B两地间的距离是60m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com