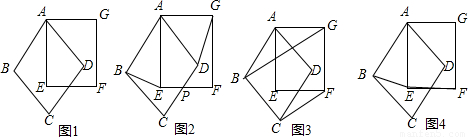
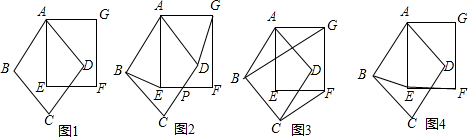
解:(1)证明:∵AB=AD,∠BAE=90°-∠EAD=∠DAG,AE=AG
∴△ABE≌△ADG,即BE=DG.
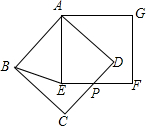
分别延长GD,BE交于点M交EF于点N,
∵∠CEN+ENM=∠MEN+∠AGD=∠BEA+∠NEM=90°
∴BE⊥GD
(∵△ABE≌△ADG,AB⊥AD,AE⊥AG,∴△ADG可以看成由△ABE绕顶点A旋转90°,即BE⊥DG.)
(2)证明:①∵AB=AG,
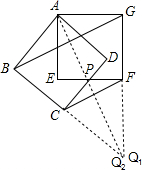
∴∠ABG=∠AGB,∠CBG=∠FGB.
∴∠GBC=∠BGF,
又∵BC=GF,
∴∠BCF=∠GFC,
又∵∠CBG+∠FGB+∠BCF+∠GFC=360°,
∴∠CBG+∠BCF=180°,即BG∥CF;
②续①又∵AB∥PC,AG∥PF,
∴∠ABG=∠PCF,∠AGB=∠PFC即△ABG∽△PCF;
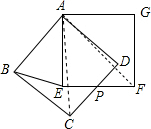
③续②连接AP交GF的延长线于Q
1,交BC的延长线于Q
2,
则
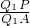
=
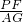
,
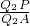
=

,而AB=AG,PC=PF
∴
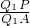
=
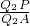
,亦有
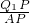
=
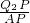
,Q
1P=Q
2P
∴Q
1,Q
2重合,即BC,AP,GF相交于点Q,△ABG与△PCF位似.
(3)连接AC,AF可证得△ABE∽△ACF,
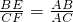
=
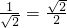
.
分析:(1)根据正方形的性质,即可得AB=AD,∠BAE=90°-∠EAD=∠DAG,AE=AG,由边角边判定方法即可证得△ABE≌△ADG,即BE=DG;∵△ABE≌△ADG,AB⊥AD,AE⊥AG,所以△ADG可以看成由△ABE绕顶点A旋转90°,即BE⊥DG;
(2)根据等边对等角即可证得BG∥CF;根据平行线的性质可的对应角相等,即可证得②△ABG∽△PCF;续②连接AP交GF的延长线于Q
1,交BC的延长线于Q
2,由位似的性质即可求得;
(3)连接AC,AF可证得△ABE∽△ACF,根据相似三角形的性质即可求得.
点评:此题考查了相似三角形与全等三角形的性质与判定,解题的关键是要注意数形结合思想的应用.还要注意辅助线的选择.

 的值.
的值.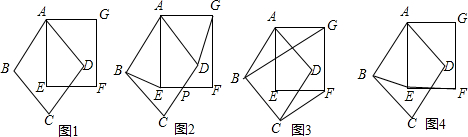



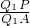 =
=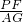 ,
,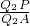 =
= ,而AB=AG,PC=PF
,而AB=AG,PC=PF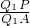 =
=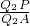 ,亦有
,亦有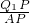 =
=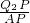 ,Q1P=Q2P
,Q1P=Q2P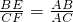 =
=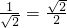 .
.

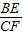 的值.
的值.